Pada sebuah segitiga siku-siku diketahui sin α = a maka nilai tan α = ….
Jawab: D
Tiga rumus fungsi trigonometri dasar adalah fungsi sinus, cosinus, dan tangen. Di mana ketiga fungsi tersebut menyetakan perbandinga sisi-sisi segitiga siku-siku dengan ketentuan seperti berikut.
Fungsi sudut sinus merupakan perbandingan nilai antara sisi depan (y) dan sisi miring (r).
Sehingga dapat diketahui bahwa panjang sisi depan adalah y = a dan sisi miring adalah r = 1. Dari nilai y dan r dapat digunakan untuk menentukan nilai sisi samping (x) dengan rumus pythagoras seperti cara penyelesaian berikut.
Mencari sisi samping (x):
x2 = r2 ‒ y2
x2 = 12 ‒ a2
x = √(1 ‒ a2)
Dapat diperoleh segitiga siku-siku dengan ukuran panjang seperti berikut.
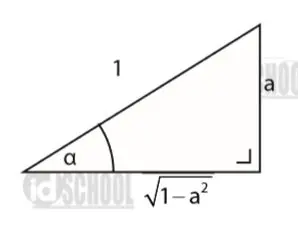
Menentukan fungsi tan:
Jadi, pada sebuah segitiga siku-siku diketahui sin α = a maka nilai tan α = a/√(1 ‒ a2)