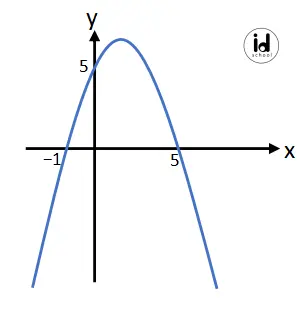
Perhatikan sketsa grafik fungsi kuadrat dan pernyataan berikut.

Pernyataan:

(1) Persamaan fungsi kuadrat tersebut y = –x² + 4x + 5.

(2) Koordinat titik potong dengan sumbu y adalah (5,0). 

(3) Persamaan sumbu simetri fungsi kuadrat tersebut x = 3. 

(4) Nilai optimum fungsi kuadrat tersebut 9. 

Pernyataan yang benar adalah …. 
A. (1) dan (3) 
B. (1) dan (4)
C. (2) dan (3) 
D. (2) dan (4)

Jawab: B.

Bentuk umum persamaan grafik fungsi kuadrat:

y = a(x – x₁)(x – x₂)

Keterangan:
x₁ dan x₂ = titik potong grafik dengan sb-x
x = titik potong grafik dengan sb-x
y = titik potong grafik dengan sb-y

Dari grafik fungsi kuadrat dapat diketahui titik potong dengan sumbu x yaitu (–1, 0) dan (5, 0) serta satu titik yang dilalui kurva yaitu (0, 5). Sehingga dapat diketahui bahwa x₁ = –1, x₂ = 5, x = 0, dan y = 5.

Substitusi nilai x₁ = –1, x₂ = 5, x = 0, dan y = 5 ke persamaan y = a(x – x₁)(x – x₂) untuk mendapatkan nilai a.

1) Menentukan nilai a:

5 = a(0 – (–1))(0 – 5)

5 = a × 1 × (–5)  

5 = –5a  

a = ⁵/_–5 = –1

2) Menentukan persamaan grafik fungsi kuadrat:  

y = a(x – x₁)(x – x₂)

y = –1(x – (–1))(x – 5)

y = –1(x + 1)(x – 5)

y =  –1(x² – 5x + x – 5)

y =  –1(x² – 4x – 5)

y =  –x² + 4x + 5

Sehingga,

(1) Persamaan fungsi kuadrat tersebut y = –x² + 4x + 5 → BENAR

(2) Koordinat titik potong dengan sumbu y adalah (5, 0) → SALAH, seharusnya (0, 5)

(3) Persamaan sumbu simetri fungsi kuadrat tersebut x = 3 → SALAH, seharusnya x_p = –⁴/_2(–1) = ⁴/₂ = 2

(4) Nilai optimum fungsi kuadrat tersebut 9 → BENAR, nilai optimum fungsi kuadrat = y_p =  –x² + 4x + 5 = –(2)² + 4(2) + 5 = –4 + 8 + 5 = 9

Jadi, pernyataan yang benar adalah (1) dan (4)