Dengan induksi matematika,
Jawab: B
Notasi Ʃ (sigma) merupakan notasi penjumlahan, untuk Ʃnp = 1 1/3p membentuk deret Ʃnp = 1 1/3p = 1/31 + 1/32 + 1/33 + … + 1/3n = 1/3 + 1/9 + 1/27 + … + 1/3n
Deret yang dihasilkan merupakan deret geometri dengan rasio r = 1/3. Rumus jumlah n suku pertama deret geometri untuk rasio -1 < r < 1 menggunakan persamaan berikut.
Deret 1/3 + 1/9 + 1/27 + … + 1/3n memiliki,
- Suku pertama: a = 1/3
- Rasio: r = 1/3
Sehingga, rumus deret 1/3^p adalah persamaan Sn berikut.
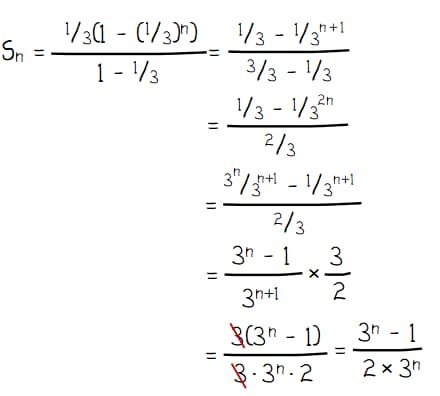
Selanjutnya, Sn untuk rumus deret 1/3^p adalah di atas akan ditunjukkan benar dengan induksi matematika melalui dua langkah pembuktian berikut.
Langkah 1: buktikan benar untuk n = 1
Bukti:
Dari hasil yang diperoleh S1 = jumlah satu suku pertama = 1/3. Sehingga dapat disimpulkan bahwa rumus Sn benar untuk n = 1.
Langkah 2: asumsikan benar untuk n = k dan buktikan benar untuk n = k + 1
Asumsikan Sn benar untuk n = k:
Selanjutkanya perlu dibuktikan Sn rumus deret 1/3^p adalah benar untuk n = k + 1 yang hasilnya akan memenuhi persamaan berikut.

Terbukti benar untuk n = 1 dan n = k+1. Jadi, rumus deret 1/3^p adalah (3^n − 1)/(2 × 3^n)