Rumus dan Materi Induksi Matematika +Contoh Soal dan Bahas

Materi induksi matematika berkaitan dengan cara membuktikan pernyataan matematika. Induksi matematika adalah suatu cara untuk membuktikan kebenaran dari suatu pernyataan matematika yang berhubungan dengan bilangan asli. Ada dua langkah pemubuktian induksi matematika. Langkah pertama adalah buktikan n = 1 benar. Langkah kedua adalah asumsikan n = k benar dan buktikan n = k + 1 benar.

Bagaimana langkah pembuktian induksi matematika? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Daftar isi:

Langkah-langkah Pembuktian Induksi Matematika

Induksi matematika merupakan teknik untuk membuktikan suatu pernyataan matematika yang didefinisikan: pada bilangan asli n adalah bernilai benar untuk semua nilai n yang lebih besar atau sama dengan sebuah bilangan asli tertentu.

Prinsip pembuktian dengan teknik ini memiliki efek domino. Di mana pada saat domino disusun sejajar dengan jarak tertentu, satu ujung domino jatuh akan membuat domino-domino lain ikut jatuh.

Prinsip langkah pembuktian materi induksi matematika

Dari prinsip efek domino tersebut dapat disimpulkan dua langkah pembuktian pernyataan matematika. Langkah pembuktian ini lah yang menjadi bahasan materi induksi matematika.

Langkah pembuktian pernyataan matematika dengan induksi matematika selalu menggunakan dua langkah berikut.

Buktikan benar untuk n = 1
Asumsikan benar untuk n = k, kemudian tunjukkan bahwa pernyataan benar untuk n = k + 1

Langkah pertama pembuktian disebut sebagai langkah dasar (basis step). Sedangkan langkah kedua pembuktian disebut dengan langkah induktif (inductive step).

Meski hanya menggunakan dua langkah pembuktian, namun setiap soal memiliki cara pengerjaan yang berbeda-beda. Bagaimana penggunaan dua langkah pembuktian tersebut akan ditunjukkan melalui penyelesaian beberapa bentuk soal di bawah.

3 Jenis Pembuktian pada Materi Induksi Matematika

Induksi matematika digunakan untuk membuktikan pernyataan yang khusus menyangkut bilangan asli. Ada tiga bentuk pembuktian yaitu deret (rumus jumlah barisan), keterbagian, dan ketidaksamaan. Setiap bentuk pembuktian selalu dilakukan melalui dua langkah pembuktian.

Bagaimana pembuktian dilakukan untuk ketiga bentuk pembuktian tersebut terdapat pada masing-masing ulasan di bawah.

1) Pembuktian deret (Rumus jumlah barisan)

Deret adalah penjumlahan suku-suku dari suatu barisan yang memiliki suatu pola. Rumus jumlah barisan aritmatika yang dinyatakan dalam Sn dapat dibuktikan menggunakan dua langkah pembuktian induksi matematika. Bagaimana langkah pembuktiannya terdapat pada penyelesaian contoh soal di bawah.

Perhatikan contoh soal dan pembahasan berikut.

Soal 1:

Buktikan bahwa Ʃ_i=1ⁿ i =

n(n + 1)2

benar!

Bukti:
Pembuktian pernyataan matematika Ʃ_i=1ⁿ i = ^{n(n + 1)}/₂ menggunakan dua langkah pembuktian induksi matematika. Bagaimana langkah pembuktiannya terdapat pada penjelasan di bawah.

Langkah 1:
Akan dibuktikan benar untuk n = 1.

Diketahui persamaan notasi Ʃ_i=1ⁿ i = 1 + 2 + 3 + …. + n dan rumus Sn = ¹/₂n(n + 1).

Untuk n = 1 maka Ʃ_i=1¹ i = 1 dan Sn = ¹/₂×1×(1 + 1) = 1. Sehingga pernyataan Ʃ_i=1ⁿ i = ¹/₂n(n + 1) terbukti benar untuk n = 1.

Langkah 2:
Asumsikan benar untuk n = k dan dibuktikan benar untuk n = k + 1.

2a) Asumsikan benar untuk n = k:
Caranya dilakukan dengan substitusi (mengganti) nilai n dengan nilai k seperti yang dilakukan pada cara berikut.

Ʃ_i=1^k i =

k(k + 1)2

→ benar (asumsi)

2b) Dibuktikan benar untuk n = k + 1:
Caranya dilakukan dengan substitusi (mengganti) nilai n dengan nilai k + 1 untuk persamaan di ruas kiri dan kanan.

Persamaan saat n = k + 1 untuk ruas kanan:

Sn =

(k + 1)(k + 2)2

Selanjutnya buktikan bahwa hasil substitusi nilai n = k + 1 untuk persamaan ruas kiri sama dengan persamaan di ruas kanan di atas. Caranya dengan melakukan operasi hitung aljabar seperti yang terdapat pada pembuktian di bawah.

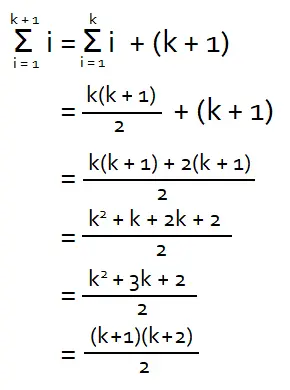
Contoh langkah pembuktian induksi matematika

Hasil akhir saat n = k + 1 untuk ruas kiri sama dengan ruas kanan. Dengan demikian terbukti pernyataan matematika untuk n = k + 1 benar.

Kesimpulan: terbukti benar untuk n = 1 dan n = k + 1, sehingga pernyataan matematika tersebut TERBUKTI benar.

2) Pembuktian keterbagian

Makna keterbagian di sini adalah habis dibagi bukan hanya dapat dibagi. Pernyataan ‘a habis dibagi b’ bersinonim dengan a kelipatan b, b faktor dari a, dan b membagi habis a.

Jika p habis dibagi a dan q habis dibagi a, maka (p + q) juga habis dibagi a. Contohnya, 4 habis dibagi 2 dan 6 habis dibagi 2, maka (4 + 6) juga habis dibagi 2.

Cara pembuktian keterbagian tidak jauh berbeda dengan pembuktian deret. Di mana ada dua langkah yang harus dilakukan yaitu langkah dasar dan induktif. Bagaimana pembuktian keterbagian menggunakan induksi matematika terdapat pada penyelesaian contoh soal di bawah.

Soal 2: Buktikan bahwa 7ⁿ − 1 habis dibagi 6 untuk sebarang bilangan asli n!

Bukti:

Setiap pembuktian dengan induksi matematikan selalu diawali dengan langkah dasar yaitu dibuktikan benar untuk n = 1.

Langkah 1: dibuktikan benar untuk n = 1

Substitusi nilai n = 1,
7ⁿ − 1 = 7¹ − 1
= 7 − 1
= 6

Di sini hasil akhir yang diperoleh saat n = 1 adalah 6 (habis di bagi 6). Sehingga pernyataan matematika 7ⁿ − 1 terbukti benar untuk n = 1.

Selanjutnya memeriksa langkah induksi yaitu diasumsikan benar untuk n = k dan dibuktikan benar untuk n = k + 1.

Langkah 2: asumsikan benar untuk n = k dan dibuktikan benar untuk n = k + 1.

Asumsikan benar untuk n = k, sehingga 7^k − 1 benar habis dibagi 6.

Dibuktikan benar untuk n = k + 1:
7^{k + 1} − 1 = 7 ∙ 7^k − 1
= (6 + 1) ∙ 7^k − 1
= 6 ∙ 7^k + 7^k − 1
= (6 ∙ 7^k) + (7^k − 1)

Dari persamaan terakhir, 6 ∙ 7^k merupakan bilangan kelipatan 6. Sehingga bilangan tersebut pasti habis dibagi 6. Sementara bilangan 7^k − 1 telah diasumsikan habis dibagi enam.

Kesimpulan: langkah dasar dan induktif dipenuhi sehingga TERBUKTI bahwa 7ⁿ − 1 habis dibagi 6 untuk sebarang bilangan asli n.

3) Pembuktian ketidaksamaan

Ketidak samaan memiliki sifat-sifat yang juga berlaku pada materi induksi matematika. Sifat-sifat ketidaksamaan meliputi beberapa poin berikut.

Sifat transitif:
a > b > c → a > c
a < b < c → a < c

a < b dan c > 0 → ac < bc
a > b dan c > 0 → ac > bc

a < b → a + c < b + c
a > b → a + c > b + c

Untuk melihat bagaimana pembuktian ketidaksamaan dengan materi induksi matematika, perhatikan cara penyelesaian soal di bawah.

Soal 3: Buktikan bahwa ketaksamaan n < 2ⁿ untuk sebarang bilangan asli n!

Bukti:
Pembuktian ketidaksamaan dengan induksi matematika juga meliputi dua langkah seperti uraian berikut.

Langkah 1: dibuktikan benar untuk n = 1

Substitusi nilai n = 1 pada ketidaksamaan n < 2ⁿ,
1 < 2¹
1 < 2 (benar)

Langkah 2: asumsikan benar untuk n = k dan dibuktikan benar untuk n = k + 1.

Asumsikan benar untuk n = k:
n < 2ⁿ
k < 2^k (benar)

Ditunjukkan benar untuk n = k + 1,
k < 2^k (telah diasumsikan benar)
k + 1 < 2^k + 1

Perhatikan bahwa, nilai 1 akan selalu lebih kecil atau sama dengan 2^k untuk nilai k = 0, 1, 2, 3, dst. Dengan demikian dapat disimpulkan 1 ≤ 2^k.

Sehingga,
k + 1 < 2^k + 1 ≤ 2^k + 2^k = 2 ∙ 2^k = 2^{k + 1}
k + 1 < 2^{k + 1}

Diperoleh ketidaksamaan k + 1 < 2^{k + 1} bernilai benar berdasarkan asumsi bahwa k < 2^k benar.

Kesimpulan: terbukti benar untuk n = 1, diasumsikan benar untuk n = k, dan terbukti benar untuk n = k + 1. Jadi, TERBUKTI benar bahwa n < 2ⁿ benar untuk sembarang bilangan asli n.

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.

Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih!

Contoh 1 – Soal Induksi Matematika Keterbagian

Dengan pembuktian induksi matematika, rumus Un yang dapat dibagi 3 adalah ….
A. Un = n³ + n²
B. Un = n³ + 2n²
C. Un = n³ + 2n
D. Un = n³ + 3n
E. Un = n³ + 4n

Pembahasan:
Pertama, periksa rumus Un pada pilihan ganda yang memenuhi langkah dasar (saat n = 1 bernilai benar)

A.	U₁ = 1³ + 1² = 2	salah
B.	U₁ = 1³ + 2(1²) = 3	benar
C.	U₁ = 1³ + 2(1) = 3	benar
D.	U₁ = 1³ + 3(1) = 4	salah
E.	U₁ = 1³ + 4(1) = 5	salah

Ada dua rumus Un yang memenuhi langkah dasar yaitu Un = n³ + 2n² dan Un = n³ + 2n.

Selanjutnya, gunakan langkah induktif untuk kedua rumus Un untuk menentukan rumus Un yang dapat dibagi 3 dari kedua rumus Un tersebut.

B.) Untuk Un = n³ + 2n²

Asumsikan benar untuk n = k:
U_k = k³ + 2k² habis dibagi tiga

Dibuktikan benar untuk n = k + 1:
U_{k + 1} = (k + 1)³ + 2(k + 1)²
U_{k + 1} = k³ + 3k² + 3k + 1 + 2k² + 2k + 2
U_{k + 1} = k³ + 2k² + 3k² + 3k + 3 + 2k
U_{k + 1} = k³ + 2k² + 3(k² + k + 1) + 2k

Berdasarkan asumsi, k³ + 2k² habis dibagi tiga. Sementara 3(k² + k + 1) merupakan bilangan kelipatan tiga sehingga pasti habis dibagi tiga.

Namun untuk 2k tidak selalu dapat habis dibagi tiga, sehingga pernyataan tidak terbukti benar untuk n = k + 1. Dengan demikian rumus Un = n³ + 2n² tidak terbukti habis dibagi tiga.

C.) Untuk U_n = n³ + 2n

Asumsikan benar untuk n = k:
U_k = k³ + 2k habis dibagi tiga
Dibuktikan benar untuk n = k + 1,
U_{k + 1} = (k + 1)³ + 2(k + 1)
U_{k + 1} = k³ + 3k² + 3k + 1 + 2k + 2
U_{k + 1} = k³ + 2k + 3k² + 3k + 3
U_{k + 1} = k³ + 2k + 3(k² + k + 1)

Berdasarkan asumsi, k³ + 2k habis dibagi tig. Sedangkan 3(k² + k + 1) merupakan bilangan kelipatan tiga sehingga pasti habis dibagi tiga. Penjumlahan sama-sama habis dibagi tiga, sehingga dapat disimpulkan bahwa rumus Un = n³ + 2n terbukti habis dibagi tiga.

Jadi, rumus Un yang dapat dibagi 3 adalah U_n = n³ + 2n.

Jawaban: C

Contoh 2 – Soal Pembuktian Deret

Diketahui 2 + 6 + 10 + 14 + …. + (4n − 2). Dengan induksi matematika, rumus deret tersebut adalah ….
A. ¹/₂n²
B. 2n²
C. n² + n
D. ¹/₂(n² + n)
E. ¹/₂n² + n

Pembahasan:
Dari deret 2 + 6 + 10 + 14 + …. + (4n − 2) dapat diketahi bahwa deret tersebut merupakan deret arimatika karena setiap kenaikan sukunya memiliki nilai beda yang sama yaitu b = 4.

Rumus jumlah suku n suku pertama deret aritmatika:

(a + U_n)

(2 + 4n − 2)

× 4n

= 2n²

Diperoleh rumus deret S_n = 2n², untuk kebenaran dari rumus tersebut dibuktikan dengan induksi matematika.

1) Dibuktikan benar untuk n = 1
S₁ = 2(1)² = 2×1 = 2, terbukti benar untuk n = 1

2a) Asumsikan benar untuk n = k:
2 + 6 + 10 + … + (4k − 2) = 2k² benar

2b) Dibuktikan benar untuk n = k + 1: akan dibuktikan pernyataan 2 + 6 + 10 + … + (4(k + 1) − 2) = 2(k + 1)²