Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B sejauh 40 mil dengan arah 30^o

Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B sejauh 40 mil dengan arah 30^o dari A kemudian berputar haluan dilanjutkan ke pelabuhan C sejauh 60 mil dengan arah 150^o dari B.

Jarak terdekat dari pelabuhan A dan C adalah ….
A. 20√2 mil
B. 20√3 mil
C. 20√5 mil
D. 20√7 mil
E. 20√11 mil

Jawab: D

Berdasarkan keterangan yang diberikan pada soal, titik-titik ABC membentuk segitiga dengan ukuran seperti berikut.

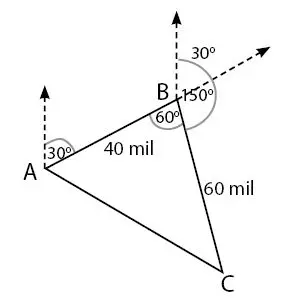
Dari segitiga ABC di atas, diketahui panjang AB, BC, dan besar ∠ABC. Jarak terdekat dari pelabuhan A dan C sama dengan panjang AC pada segitiga ABC. Panjang AC dapat diketahui dengan rumus aturan cosinus.

Rumus aturan cosinus:
AC² = AB² + BC² ‒ 2×AB×BC×cos ∠ABC

Menghitung jarak terdekat antara pelabuhan A ke pelabuhan C:
AC² = AB² + BC² ‒ 2×AB×BC×cos 60^o
AC² = 40² + 60² ‒ 2×40×60×¹/₂
AC² = 1.600 + 3.600 ‒ 2.400 = 2.800
AC = √2.800
AC = √(400×7) = √400 × √7 = 20√7 mil

Jadi, jarak terdekat dari pelabuhan A ke C adalah 20√7 mil.