Sebuah kubus memiliki ukuran panjang rusuk 14 cm. Misalkan sebuah kerucut berada di dalam kubus sedemikian rupa sehingga alas kerucut menyinggung bidang alas serta titik puncak kerucut tepat menyentuk bidang atas kubus.
Untuk π = 22/7 luas permukaan kerucut tersebut adalah … cm2
(A) 77
(B) 154
(C) 77(√5+1)
(D) 154(√5+1)
(E) 154(√5+2)
Jawab: (D)
Dari soal diketahui bahwa: sebuah kubus memiliki ukuran panjang rusuk 14 cm dan sebuah kerucut yang menyinggung bagian alas dan atas kubus. Gambaran kubus dan kerucut yang sesuai dengan keterangan pada soal terdapat seperti bentuk berikut.
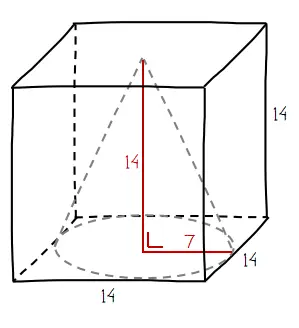
Lkerucut = πr2 + πrs
Keterangan:
π = 22/7
r = jari-jari alas kerucut
s = garis pelukis kerucut
Dari soal dapat diketahui jari-jari alas kerucut = r = 7 cm. Sedangkan panjang garis pelukis kerucut belum diketahui, sehingga perlu dihitung terlebih dahulu.
Menghitung garis pelukis kerucut:
s2 = 72 + 142
s2 = 49 + 196 = 245
s = √245
s = √(49×5) = 7√5 cm
Menghitung luas kerucut:
Lkerucut = πr2 + πrs
= 22/7×72 + 22/7×7×7√5
= 154 + 154√5
= 154(1+√5)
Jadi, luas permukaan kerucut tersebut adalah 154(1+√5) = 154(√5+1) cm2 (D).