UTBK 2025/Penalaran Matematika
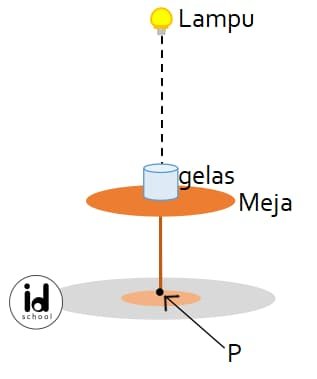
Sebuah lampu tergantung di langit-langit suatu ruangan, tepat di atas suatu meja bundar. Jari-jari meja tersebut 1,5 m dan jari-jari bayangannya di lantai adalah 2,5 m. Sebuah gelas berbentuk tabung diletakkan tepat di tengah meja.

Soal-soal

• Soal 1
• Soal 2
• Soal 3
• Soal 4

Soal 1

Tinggi meja adalah 0,8 m. Tinggi lampu dari lantai adalah … m.
(A) 1,5
(B) 1,8
(C) 2,0
(D) 2,4
(E) 2,5

Pembahasan:
Diketahui jari-jari meja = 1,5 m; jari-jari bayangan meja di lantai = 2,5 m, dan tinggi meja = 0,8 m. Tinggi lampu dari lantai dapat dicari menggunakan rumus kesebangunan.

Perhatikan informasi ukuran-ukuran yang diketahui melalui gambar di bawah.

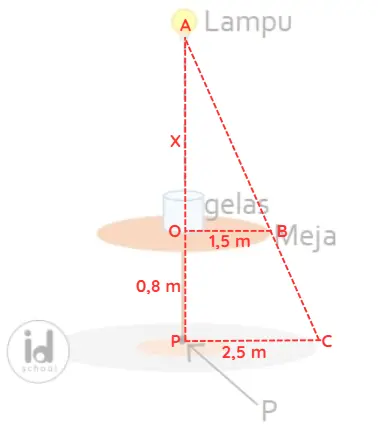
Dari segitiga ABO dan segitiga ACP dapat dibentuk kesebangunan seperti persamaan di bawah.

5x = 3(0,8 + x)

5x = 2,4 + 3x

2x = 2,4

Tinggi lampu dari lantai adalah PA = AO + OP = x + 0,8 m = 1,2 m + 0,8 m = 2,0 m. Jadi, tinggi lampu dari lantai adalah 2,0 meter.

Jawab: (C)

Soal 2

Misalkan tinggi lampu 2,5 m dan tinggi gelas 10 cm. Perbandingan luas bagain atas gelas dan bayangannya di meja adalah 1 : ….

Pembahasan:
Diketahui jari-jari meja = 1,5 m; jari-jari bayangan meja di lantai = 2,5 m; dan tinggi lampu dari lantai = 2,5 meter.

Dari informasi yang diketahui panjang jari-jari bayangan meja di lantai = 2,5 meter dan tinggi lampu dari lantai = 2,5 meter. Sehingga dapat disimpulkan bahwa segitiga yang dibentuk oleh titik pada lampu, titik pusat bayangan meja, dan titik terluar bayangan meja merupakan segitiga siku-siku sama kaki.

Dengan begitu, segitiga yang dibentuk oleh titik pusat meja, titik terluar meja, dan titik pada lampu juga segitiga siku-siku sama kaki. Diketahui panjang jari-jari meja = 1,5 meter maka jarak titik pada lampu ke titik pada pusat meja = 1,5 meter.

Informasi ukuran-ukurannya disajikan lebih jelas melalui gambar di bawah.

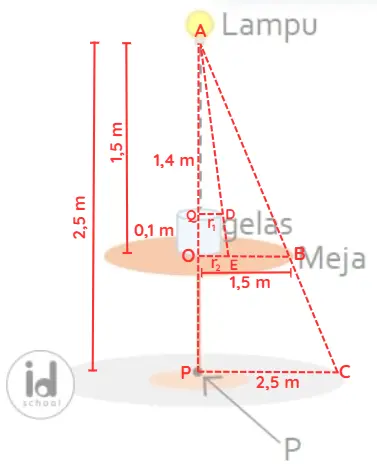
Dari segitiga AQD dan segitiga AOE dapat dibentuk persamaan kesebangunan seperti berikut.

Perbandingan jari-jari bagian atas gelas dan bayangannya adalah r₁ : r₂ = 14 : 15 sehingga 15r₁ = 14r₂ atau untuk jari-jari bagian atas gelas adalah r₁ maka jari-jari bayangan gelas adalah r₂ = ¹⁵/₁₄r₁.

Menentukan besar perbandingan:

Bagian atas gelas berbentuk lingkaran, luasnya adalah πr². Perbandingan luas bagain atas gelas dan bayangannya di meja dapat diketahui melalui cara di bawah.

Jadi, perbandingan luas bagain atas gelas dan bayangannya di meja adalah 1 : (15/14)².

Jawab: (B)

Soal 3

Ana yang tinggi badannya 150 cm berdiri di titik A yang berjarak 3 m dari titik P. Misalkan C adalah ujung bayangan Ana. Kemudian Ana bergerak ke titik B yang berjarak 5 m dari titik P sehingga ujung bayangan Ana sekarang adalah C’. Jika tinggi lampu adalah 2,5 m dan ∠PAB = 90^o, jarak CC’ adalah … m.
(A) 9  
(B) 9,5  
(C) 10
(D) 10,5  
(E) 11

Pembahasan:
Berdasarkan informasi yang diberikan pada soal dapat digambar ilustrasi berikut.

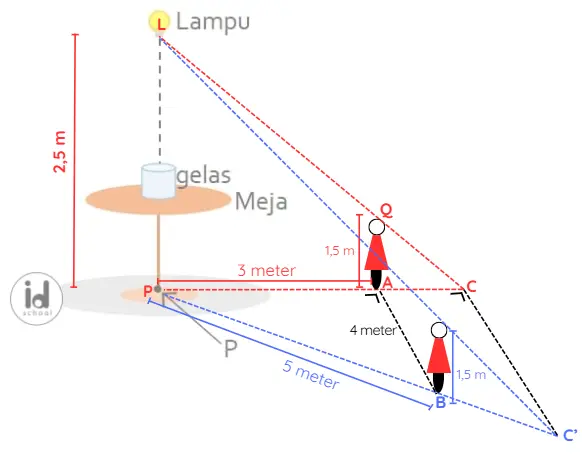
Diketahui panjang PA = 3 meter dan PB = 5 meter. Segitiga PAB merupakan segitiga siku-siku. Dengan Tripel Pythagoras dapat diketahui panjang AB secara sepat yaitu AB = 4 meter.

Selanjutnya, dari kesebangunan segitiga PCL dan segitiga ACQ dapat dibentuk persamaan di bawah:

5AC = 3(3 + AC)

5AC = 9 + 3AC

2AC = 9

Perhatikan segitiga PCC’ dan segitiga PAB! Dari kesebangunan dua segitiga tersebut diperolah persamaan berikut.

CC’ = 2,5 × 4 = 10

Jadi, jarak CC’ adalah 10 meter.

Jawab: (C)

Soal 4

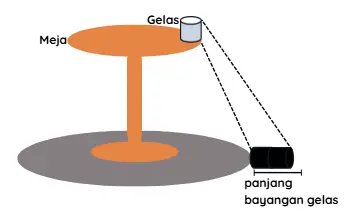
Misal diketahui tinggi lampu adalah 2,5 m. Jika gelas yang semula berada di tengah meja digeser sehingga tepat berada di tepi meja, panjang bayangan gelas di lantai adalah … m.

Pembahasan:
Perhatikan ilustrasi gambar berdasar informasi yang diberikan pada soal nomor 4 berikut.

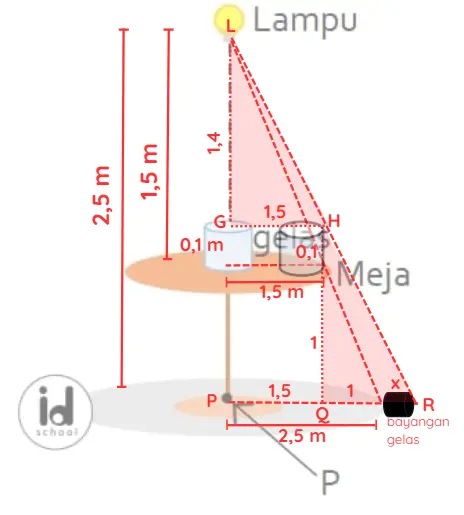
Perhatikan segitiga LGH! Panjang LG = jarak lampu ke meja – tinggi gelas = 1,5 m – 0,1 m = 1,4 m dan panjang GH = jari-jari meja = 1,5 m.

Perhatikan segitiga HQR! Panjang HQ = jarak meja ke lantai + tinggi gelas = (2,5 m – 1,5 m) + 0,1 m = 1,1 m. Panjang jari-jari bayangan meja = 2,5 m dan jarak titik P ke Q = panjang jari-jari meja = 1,5 m; maka jarak titik Q ke bagian terluar bayangan meja = 2,5 m – 1,5 m = 1 m. Misalkan panjang bayangan gelas = x m, panjang QR = 1 + x.

Segitiga LGH dan segitiga HQR sebangun sehingga dapat dibentuk persamaan berikut.

1,4(1 + x) = 1,1 × 1,5

1,4 + 1,4x = 1,65

1,4x = 0,25

Jadi, panjang bayangan gelas di lantai adalah 25/140 m.

Jawab: (D)