UTBK 2019/PK
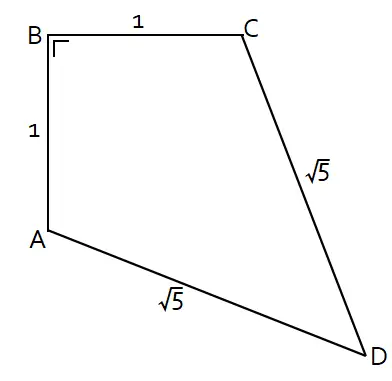
Segi empat ABCD merupakan layang-layang seperti pada gambar. Jika AB = 1 dan AD = √5 maka luas layang-layang tersebut dalam satuan luas adalah ….
(A) 3/2
(B) 2
(C) 3
(D) √5
(E) 2√5 + 2
Jawab: (B)
Cara menghitung luas layang-layang dapat menggunakan rumus layang-layang L = 1/2(d1 × d2) di mana d1 dan d2 adalah panjang diagonal layang-layang. Dari soal belum diketahui panjang kedua diagonal layang-layang sehingga nilainya perlu dihitung terlebih dahulu.
Diagonal layang-layang adalah ruas garis AC dan BD. Panjang kedua diagonal layang-layang tersebut dapat dihitung menggunakan Teorema Pythagoras.
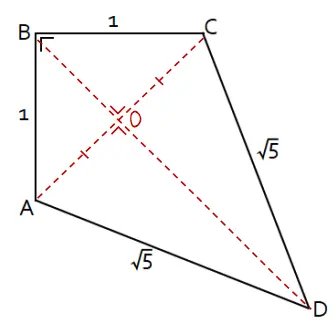
1) Menghitung panjang AC:
AC = √(AB2 + BC2)
AC = √(12 + 12) = √2
2) Menghitung panjang BO:
BO = √(BC2 – OC2) = √(BC2 – (1/2AC)2)
BO = √(12 – (1/2√2)2) = √(1 – 1/2)
BO = √1/2 = 1/2√2
3) Menghitung panjang OD:
BO = √(CD2 – OC2) = √(CD2 – (1/2AC)2)
BO = √[(√5)2 – (1/2√2)2)]
BO = √(5 – 1/2) = √(10/2 – 1/2)
BO = √9/2 = 3/√2 = 3/2√2
Dari beberapa perhitungan yang dilakukan di atas diperoleh panjang kedua diagonal layang-layang yaitu AC = √2 dan BD = BO + OD = 3/2√2 + 1/2√2 = 2√2.
Menghitung luas layang-layang:
Luas = 1/2(d1 × d2) = 1/2(AC × BD)
Luas = 1/2(√2 × 2√2) = 1/2 × 4 = 2
Jadi, luas layang-layang tersebut dalam satuan luas adalah 2.