Semua bilangan real x yang memenuhi

(A) −2 ≤ x ≤ 2
(B) x ≤ −2 atau 0 ≤ x < 1
(C) −2 ≤ x < −¹/₂ atau 0 < x ≤ 2
(D) −2 ≤ x < −¹/₂ atau x ≥ 2
(E) x ≤ −2 atau x ≥ 2

Jawab: (C)

Pertama adalah menyederhanakan bentuk pertidaksamaan pecahan seperti yang dilakukan pada langkah berikut.

Samakan penyebutnya,

Harga nol pembilang:
8 – 2x² = 0
2x² = 8
x² = ⁸/₂ = 4
x = -2 atau x = 2

Harga nol penyebut:
x(2x + 1) = 0
x = 0 atau 2x + 1 = 0 → x = ¹/₂

Diperoleh empat nilai x yaitu -2, 0, ¹/₂, dan 2. Sehingga akan ada lima daerah dalam sebuah garis bilangan yang dibatasi oleh nilai-nilai x tersebut.

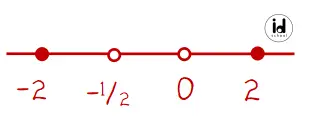
Lakukan uji titik, misalkan ambil titik 3 (sembarang), kemudian substitusi kepersamaan ^8-2x2/_{x(2x + 1)}. Akan dihasilkan nilai negatif (-), sehingga dapat disimpulkan bahwa daerah di kanan titik 2 akan menghasilkan nilai negatif.

Di sini akan dicari daerah yang menghasilkan nilai positif karena bentuk persamaan berupa lebih dari atau sama dengan nol ( ^8-2x2/_{x(2x + 1)} ≥ 0).

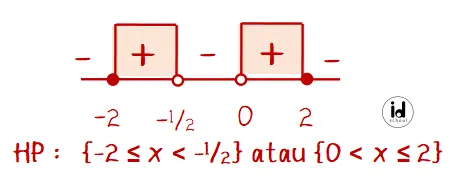
Jadi, semua bilangan real x yang memenuhi 8/x − 15/2x+1 >= 1 adalah (C) −2 ≤ x < −¹/₂ atau 0 < x ≤ 2.