Semua nilai x yang memenuhi (x + 1)(x − 2) ≥ (x – 2) adalah ….
(A)   x ≥ 1
(B)   x ≥ 2
(C)  0 ≤ x ≤ 2
(D)  x ≤ 0 atau x ≥ 2
(E)   x ≤ 1 atau x ≥ 2

Jawab: (D)

Pindah fungsi di sebelah kanan ke sebelah kiri sehingga diperoleh pertidaksamaan dengan fungsi 0 di sebelah kiri.

(x + 1)(x − 2) ≥ (x – 2)
x² − x − 2 − (x − 2) ≥ 0
x² − 2x ≥ 0
x(x − 2) ≥ 0

Titik kritis atau pembuat nol dicapai saat persamaan x(x − 2) = 0. Dari persamaan tersebut dapat diketahui dua nilai x pembuat nol yaitu x = 0 atau x = 2.

Dua nilai titik kritis tersebut membagi sebuah garis bilangan menjadi tiga daerah yaitu daerah di sebelah kiri 0, antara 0 dan 2, serta daerah di kanan 2.

Ketiga daerah pada garis bilangan tersebut memiliki nilai positif/negatif. Untuk mengetahuinya lakukan pengujian titik. Misalkan ambil x = 1 yang berada di daerah antara 0 sampai 2. Kemudian substitusikan ke fungsi f(x) = x(x − 2).

Mencari hasil substitusi x = 1:

f(x) = x(x − 2)

f(1) = 1×(−1) = −1

Dari hasil perhitungan diperoleh hasil f(−1) = −1. Sehingga dapat disimpulkan bahwa daerah yang memuat nilai x = −1 adalah daerah negatif. Dengan begitu, dua daerah di sampingnya adalah positif.

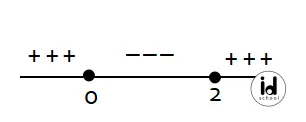
Di sini, bentuk pertidaksamaan adalah x(x − 2) ≥ 0. Sehingga semua nilai x yang memenuhi (x + 1)(x − 2) ≥ (x – 2) adalah daerah-daerah positif.

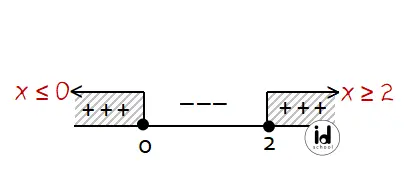
Jadi, semua nilai x yang memenuhi (x + 1)(x − 2) ≥ (x – 2) adalah (D) x ≤ 0 atau x ≥ 2.