Semua nilai x yang memenuhi
(A) −2 < x < 0
(B) x < −2 atau x > 0
(C) 0 < x ≤ 2
(D) x < 0 atau x > 2
(E) x < 0 atau x ≥ 2
Jawab: (A)
Semua nilai x yang memenuhi x^2-3x+1/x^2+2x <= -2/x+2 adalah himpunan penyelesaian dari pertidaksamaan tersebut. Cara menentukan himpunan penyelesaian pertidaksamaan tersebut dilakukan dengan beberapa langkah berikut.
Pertama, sederhanakan bentuk petidaksamannya terlebih dahulu. Di mana ruas kanan perlu dibawa ke bilangan nol dengan cara memindah fungsi pada ruas kanan ke ruas kiri seperti berikut.
Harga nol pembilang: x2 – x + 1 = 0
Persamaan kuadrat x2 – x + 1 = 0 tidak bisa difaktorkan karena nilai diskriminan kurang dari nol (D < 0). Artinya, grafik fungsi kuadrat tersebut tidak memiliki titik potong dengan sumbu-x.
Nilai a untuk persamaan kuadrat x2 – x + 1 = 0 adalah 1 sehingga a > 0. Fungsi kuadrat dengan D < 0 dan a > 0 memiliki kondisi definit positif yaitu kondisi di mana fungsi kuadrat selalu menghasilkan nilai positif (grafik terletak di atas sumbu-x).
Kesimpulannya, pembilang selalu memiliki nilai positif.
Pertidaksamaan yang dimiliki adalah kurang dari atau sama dengan (≤). Saat pembilang bernilai positif maka penyebut harus memiliki nilai negatif (kurang dari nol).
Perlu diingat bahwa penyebut tidak boleh nol. Sehingga semua nilai x yang memenuhi x^2-3x+1/x^2+2x <= -2/x+2 adalah himpunan penyelesaian dari x(x + 1) < 0.
Harga nol penyebut:
x(x + 1) = 0
x = 0 atau x = -1
Dua nilai x tersebut akan membagi garis bilangan menjadi tiga daerah. Lakukan pengujian titik untuk mengetahui daerah positif/negatif dari ketiga daerah tersebut. Himpunan penyelesaian untuk pertidaksamaan x(x + 1) < 0 adalah daerah dengan nilai negatif karena memiliki bentuk pertidaksamaan kurang dari.
Setelah melakukan pengujian titik dapat diketahui bahwa daerah negatif nerada di antara -2 dan 0. Semua nilai x yang memenuhi x^2-3x+1/x^2+2x <= -2/x+2 adalah nilai-nilai yang berada selang tersebut.
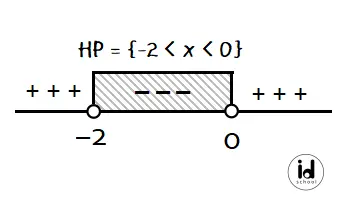
Jadi, semua nilai x yang memenuhi x^2-3x+1/x^2+2x <= -2/x+2 adalah …. (A) −2 < x < 0.