Seorang pedagang minuman memiliki modal Rp 200.000,00. Ia berencana membeli 2 jenis minuman. Minuman A dibeli dengan harga Rp6.000,00 per botol dan dijual untung Rp500,00 per botol.
Minuman B dibeli dengan harga Rp8.000,00 per botol dan dijual dengan untung Rp1.000,00 per botol. Bila tempatnya hanya mampu menampung 30 botol minuman maka keuntungan maksimum yang dapat diraih adalah ….
A. Rp30.000,00
B. Rp25.000,00
C. Rp20.000,00
D. Rp16.000,00
E. Rp15.000,00
Jawab: B
Secara ringkas, langkah menyelesaikan soal program linear terdapat pada beberapa nomor di bawah.
- Membuat model matematika yang sesuai dengan soal yang diberikan.
- Menentukan daerah layak
- Menentukan titik pojok dari daerah layak
- Menghitung nilai fungsi tujuan untuk menentukan nilai minimum/maksimum, tergantung dari soal yang diberikan
Langkah pertama, kita perlu memodelkan soal cerita yang diberikan pada soal cerita pada soal. Untuk melakukannya perlu melakukan pemisalan variabel untuk banyak minuman jenis A dan B milik pedagang.
Misalkan:
x = banyaknya minuman jenis A
y = banyaknya minuman jenis B
Berdasar informasi pada soal dapat diperoleh ringkasan nilai-nilainya dalam tabel berikut.

Dari tabel di atas dapat memudahkan untukmenyusun fungsi tujuan dan fungsi tujuan seperti berikut.
Fungsi tujuan:
memaksimalkan f(x, y) = 500x + 1.000y
Pertidaksamaan fungsi kendala:
(i) x + y ≤ 30
(ii) 6.000x + 8.000y ≤ 200.000 → 3x + 4y ≤ 100
(iii) x ≥0; (iv) y ≥ 0
Daerah yang sesuai dengan fungsi kendala:
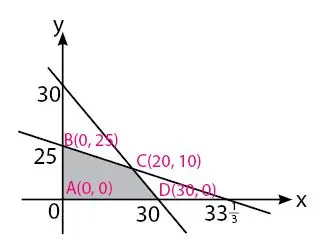
Titik A, B, dan D dapat secara mudah diketahui dengan melihat diagram gambar. Sedangkan koordinat titik C perlu dicari tahu dengan metode menentukan titik perpotongan antara garis (i) x + y ≤ 30 dan (ii) 3x + 4y ≤ 100 dengan metode substitusi/eliminasi. Cara menentukan koordinat titik C dilakukan dengan cara berikut.
Menentukan absis (x) dari titik C:

Menentukan ordinat (y) dari titik C:
20 + y = 30
y = 30 ‒ 20
y = 10
Sehingga diperoleh titik perpotongan antara garis (i) x + y ≤ 30 dan (ii) 3x + 4y ≤ 100 adalah tersebut adalah titik C (20, 10).
Selanjutnya akan dicari nilai maksimum yang dihasilkan fungsi tujuan dengan metode titik pojok. Caranya adalah substitusi nilai (x, y) pada fungsi tujuan f(x, y) = 500x + 1.000y seperti yang dilakukan pada perhitungan dalam tabel berikut.
| Titik | Nilai f(x, y) = 500x + 1.000y |
| A(0,0) | f(x, y) = 500×0 + 1.000×0 = 0 |
| B(0,25) | f(x, y) = 500×0 + 1.000×25 = 25.000 (maks) |
| C(20,10) | f(x, y) = 500×20 + 1.000×10 = 20.000 |
| D(30,0) | f(x, y) = 500×30 + 1.000×0 = 15.000 |
Jadi, keuntungan maksimum yang dapat diraih adalah Rp25.000,00