Perhatikan diagram berikut!
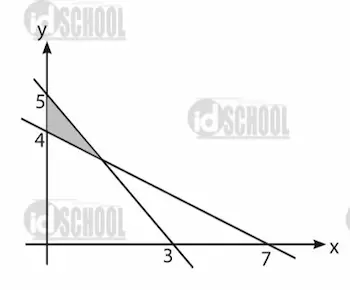
Sistem pertidaksamaan linear yang sesuai dengan daerah penyelesaian diarsir adalah ….
A. 3x + 5y ≤ 15, 4x + 7y ≥ 28, x≥0, y≥0
B. 3x + 5y ≥ 15, 4x + 7y ≤ 28, x≥0, y≥0
C. 5x + 3y ≥ 15, 4x + 7y ≥ 28, x≥0, y≥0
D. 5x + 3y ≤ 15, 4x + 7y ≤ 28, x≥0, y≥0
E. 5x + 3y ≤ 15, 4x + 7y ≥ 28, x≥0, y≥0
Jawab: E
Daerah yang diarsir dibatasi berada di kanan sumbu y (y ≥ 0), di atas sumbu (x ≥ 0), serta dua buah garis yang persamaannya belum diketahui. Dua garis yang membatasi daerah yang diarsir diketahui melalui dua titik.
Garis pertama diketahui melalui titik (3, 0) dan (0, 5). Sementara garis kedua diketahui melalui titik (7, 0) dan (0, 4). Untuk garis lurus yang melalui titik (x1, y1) dan (x2, y2) dapat ditentukan persamaannya melalui rumus garis lurus yang melalui 2 titik seperti berikut.
Rumus diatas dapat digunakan untuk menentukan persamaan kedua garis lurus yang belum diketahui.
Menentukan persamaan garis yang melalui titik (3, 0) dan (0, 5):
Daerah yang diarsir berada di bawah garis 5x + 3y = 15. Sehingga pertidaksamaan yang memenuhi adalah 5x + 3y ≤ 15.
Menentukan persamaan garis yang melalui titik (7, 0) dan (0, 4):
Daerah yang diarsir berada di atas garis 4x + 7y = 28. Sehingga pertidaksamaan yang memenuhi adalah 4x + 7y ≥ 28.
Jadi, sistem pertidaksamaan linear yang sesuai dengan daerah penyelesaian diarsir adalah 5x + 3y ≤ 15, 4x + 7y ≥ 28, x≥0, y≥0.
