Suku ketiga suatu barisan aritmetika adalah 154. Jumlah suku kelima dan suku ketujuh adalah 290.

Suku ketiga suatu barisan aritmetika adalah 154. Jumlah suku kelima dan suku ketujuh adalah 290. Jumlah 10 suku pertama sama dengan ….
A. 3.470
B. 1.735
C. 1.465
D. 1.425
E. 1.375

Jawab: C

Pada soal terdapat keterangan bahwa bentuk barisan merupakan barisan aritmatika. Rumus barisan aritmatika untuk suku ke-n dan jumlah n suku pertama dinyatakan dalam dua persamaan di bawah.

• Suku ke-n: Un = a + (n − 1)b
• Jumlah n suku pertama:

Pada soal terdapat keterangan beberapa informasi berikut.

• Suku ketiga suatu barisan aritmetika adalah 154.
  U₃ = 154
  a + 2b = 154

• Suku kelima + suku ketujuh = 290
  U₅ + U₇ = 290
  (a + 4b) + (a + 6b) = 290
  2a + 10b = 290
  a + 5b = 145

Diperoleh dua persamaan yaitu persamaan (i) a + 2b = 154 dan (ii) a + 5b = 145. Nila a dan b dapat diketahui dengan menyelesaikan SPLDV dari persamaan (i) dan (ii). Cara menentukan nilai a dan b terdapat pada langkah penyelesaian berikut.

Menentukan nilai b:
Eliminasi a dari persamaan (i) dan (ii) seperti cara berikut.

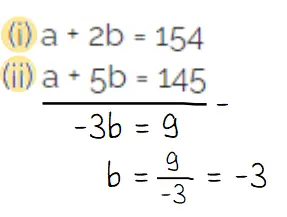
Menentukan nilai a:
Substitusi nilai b = −3 ke persamaan (ii) a + 5b = 145 untuk mendapatkan nilai a seperti berikut.

a + 5b = 145
a + 5 × (−3) = 145
a − 15 = 145
a = 145 + 15 = 160

Sehingga dapat diketahui bahwa barisan aritmatika tersebut memiliki nilai suku pertama a = 160 dan beda b = −3. Jumlah 10 suku pertama dihitung dengan jumlah n suku pertama untuk barisan aritmatika.

Menghitung jumlah 10 suku pertama (S₁₀):
S₁₀ = ¹⁰/₂(2×160 + 9×(−3))
S₁₀ = 5(320 − 27)
S₁₀ = 5 × 293 = 1.465

Jadi, jumlah 10 suku pertama barisan aritmatika tersebut sama dengan S₁₀ = 1.465