Volume benda putar yang terjadi bila daerah yang dibatasi oleh y = 2x dan parabola y = x^2 diputar sejauh 360o mengelilingi sumbu x adalah … satuan volume.
Jawab: B
Langkah-langkah untuk menghitung volume benda putar bila daerah yang dibatasi kurva y = 2x dan y = x2 diputar sejauh 360o mengelilingi sumbu x:
- Menggambar daerah yang dibatasi kurva untuk menentukan metode untuk menghitung volume benda putar mana yang akan digunakan (cakram atau kulit tabung)
- Menentukan batas pengintegralan
- Menghitung volume benda putar
Bagaimana cara menghitung volume benda putar yang terjadi bila daerah yang dibatasi oleh y = 2x dan y = x2 diputar sejauh 360o diputar sejauh 360o mengelilingi sumbu x terdapat pada langkah penyelesaian di bawah.
1) Menggambar daerah dan volume benda putar
Grafik fungsi y = 2x berupa garis lurus, sementara fungsi y = x2 menghasilkan sebuah parabola yang terbuka ke atas.
Bentuk volume benda putar yang dihasilkan oleh daerah yang dibatasi y = 2x dan y = x2 sesuai dengan gambar berikut.

2) Menentukan titik potong garis y = 2x dan kurva y = x2
Titik potong antara garis y1 = 2x dan y2 = x2 dapat diketahui dari gambar yaitu antara 0 sampai 2 pada sumbu x.
Cara lain untuk menentukan titik potong dapat menggunakan persamaan y1 = y2.
Mendapatkan titik potong:
x2 = 2x
x2 – 2x = 0
x(x – 2) = 0
Diperoleh dua nilai x yaitu x1 = 0 dan x2 = 2. Titik perpotongan tersebut akan berguna sebagai batas pengintegralan (a = 0 dan b = 2).
3) Menghitung volume benda putar
Diketahui persamaan y1 = 2x dan y2 = x2. Daerah yang dibatasi dua kurva tersebut berada pada batas a = 0 dan b = 2.
volume benda putar yang terjadi bila daerah yang dibatasi oleh y = 2x dan parabola y = x^2 diputar sejauh 360o mengelilingi sumbu x dihitung dengan cara berikut.
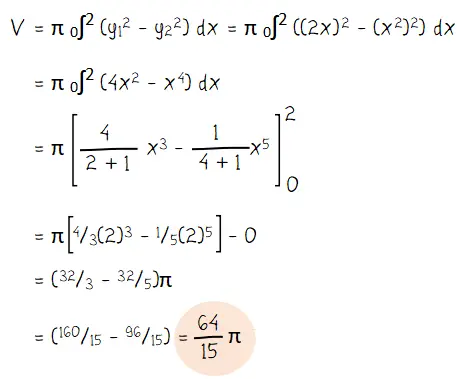
Jadi, volume benda putar yang terjadi bila daerah yang dibatasi oleh y = 2x dan parabola y = x^2 diputar sejauh 360o mengelilingi sumbu x adalah V = 64/15π satuan volume.