Ada dua bentuk rumus volume benda putar yang dapat digunakan untuk mengetahui besar volume dari suatu benda putar. Kedua rumus volume benda putar yang dapat digunakan berasal dari metode cakram dan metode kulit tabung. Dua cara menghitung volume benda putar akan menghasilkan nilai yang sama. Hanya saja, pada jenis soal tertentu akan lebih mudah dikerjakan dengan satu dari dua metode tersebut.
Bagaimana bentuk rumus volume benda putar dengan metode cakram? Bagaimana bentuk rumus volume benda putar dengan metode cincin silinder? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar isi:
Baca Juga: Cara Menghitung Luas Daerah yang Dibatasi Kurva
Volume Benda Putar
Bentuk volume benda putar berupa bangun ruang yang memiliki besar isi. Volume benda putar adalah daerah yang dibatasi suatu kurva dan kemudian diputar sejauh 360o pada suatu sumbu. Sumbu putar yang digunakan dapat berupa sumbu x, sumbu y, atau garis lain.
Misalnya sebuah garis lurus yang memotong sumbu x di titik a dan memotong sumbu y di titik b. Garis lurus tersebut beserta sumbu x dan sumbu y di kuadran I membentuk sebuah daerah berbentuk segitiga. Daerah tersebut diputar mengelilingi sumbu x sejauh 360o.
Gambar daerah yang diputar dan benda putar yang dihasilkan memiliki bentuk seperti berikut.
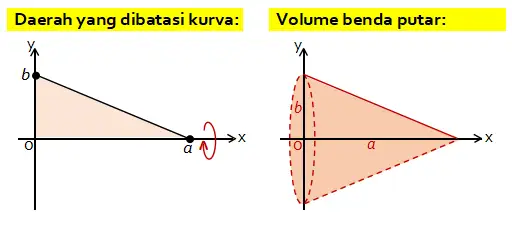
Bentuk luas daerah yang dibatasi garis lurus tersebut pada batas 0 sampai a berupa kerucut dengan panjang jari-jari b dan tinggi kerucut a. Untuk menghitung volume benda putar tersebut dapat menggunakan rumus kerucut.
Sehingga volume benda putar tersebut sama dengan Volume tabung = ⅓πr2t = ⅓πb2a = ⅓πab2 satuan volume.
Volume benda putar yang dibatasi suatu kurva memiliki bentuk yang berbeda-beda.
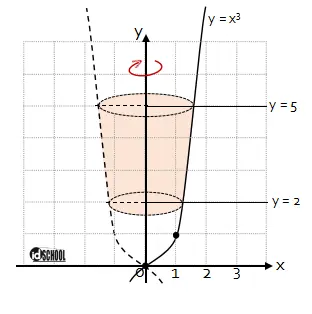
Misalnya pada volume benda putar yang dibatasi kurva y = x3 di kuadran I, garis y = 2, dan garis y = 5 yang diputar pada sumbu y. Benda putar yang dihasilkan berbentuk seperti pot bunga seperti gambar berikut.
Baca Juga: Cara Menggambar Grafik Fungsi Kuadrat y = ax^2 + bx + c
Bentuk benda putar yang dihasilkan bergantung dari kurva yang membatasi daerah luas yang diputar.
Berbagai bentuk volume benda putar dapat dihitung besar volumenya dengan rumus fungsi integral. Ada dua cara yang dapat dilakukan untuk menghitung volume dari suatu benda putar yaitu metode cakram dan kulit tabung.
Kedua cara menghitung volume benda putar tersebut dijelaskan melalui ulasan di bawah.
Rumus Volume Benda Putar Metode Cakram
Metode cakram digunakan untuk menghitung volume benda putar dengan partisi batang potongan yang dipilih tegak lurus dengan sumbu putar.
Metode cakram untuk menghitung volume menggunakan dasar rumus Volume = Luas alas × Tinggi. Pada benda putar dari luas yang diputar sejauh 360o mengeliling sumbu memiliki bentuk alas berupa lingkaran.
Diketahui bahwa rumus luas lingkaran adalah Luas = πr2 dengan r adalah jari-jari lingkaran.
Jari-jari putaran sama dengan jarak sumbu putar ke kurva yang nilainya sama dengan f(x). Sehingga rumus luas di setiap titik adalah Luas = πr2 = πf2(x). Jumlah perkalian luas dengan potongan partisi benda putar akan menghasilkan besar rumus volume untuk benda putar tersebut.
Diketahui sebuah kurva membatasi suatu daerah pada selang antara a dan b. Dengan mengambil potongan tinggi benda dx sepanjang selang dan luas daerah L = πf2(x) maka rumus volume benda putar adalah V = a ʃ b [πf2(x)] dx = π a ʃ b f2(x) dx.

Baca Juga: Aturan Sinus dan Cosinus +Contoh Penggunaannya
Rumus Volume Benda Putar Metode Kulit Tabung
Cara menghitung volume benda putar dengan metode kulit tabung dilakukan jika batang potongan sejajar dengan sumbu putar.
Dasar metode kulit tabung menggunakan luasan yang diputar terhadap sumbu dapat menghasilkan benda putar. Sehingga hasil kali luas daerah yang diputar dengan keliling putaran sama dengan volume dari benda putar.
Hasil putaran 360o membentuk lingkaran yang kelilingnya sama dengan 2πr. Untuk luas bidang yang diputar sama dengan A maka volume dari benda putar pada setiap potongan partisi adalah Volume = 2πr × A.
Jari-jari yang digunakan pada rumus volume benda putar metode kulit tabung sama dengan jarak sumbu putar ke potongan partisi dan A adalah luas bidang yang diputar.
Luas daerah yang diputar antara selang a dan b dihitung dengan rumus A = aʃb f(x) dx. Untuk jari-jari dari sumbu putar ke potongan partikel luas sama dengan x, rumus volume benda putar dengan metode kulit tabung adalah V = a ʃ b 2πx · f(x) dx = 2π a ʃ b x · f(x) dx.

Bagu Juga: Rumus Integral Fungsi Trigonometri
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Penggunaan Rumus Volume Benda Putar Metode Cakram
Volume benda putar yang terjadi jika daerah antara kurva y = –x2 + 4, sumbu X, dan garis x = 0 di kuadran I diputar mengelilingi sumbu X sejauh 360o adalah …
A. 150/15π satuan volume
B. 156/15π satuan volume
C. 160/15π satuan volume
D. 256/15π satuan volume
E. 576/15π satuan volume
Pembahasan:
Langkah pertama perlu dilakukan adalah mengetahui benda putar yang akan dihitung volumenya. Caranya dilakukan dengan menggambar grafik fungsi kuadrat y = ‒x2 + 4. Setelah itu menentukan daerah antara kurva, sumbu x, dan garis x = 0 di kuadran I.
Penyelesaian yang akan digunakan pada perhitungan di bawah adalah metode cakram. Sehingga partisi potongan benda putar dibuat tegak lurus dengan sumbu putar.
Gambar daerah yang diputar dan volume benda putar yang hasilkan sesuai dengan langkah penyelesaian berikut.

Jadi, volume benda putar yang didapat sama dengan 256/15π satuan volume.
Jawaban: D
Contoh 2 – Penggunaan Rumus Volume Benda Putar Metode Kulit Tabung
Volume benda putar yang terjadi jika daerah yang dibatasi oleh y = x2, garis y = 2, dan sumbu y diputar mengelilingi sumbu y sejauh 360o adalah ….
A. π satuan volume
B. 1,5π satuan volume
C. 2π satuan volume
D. 2,5π satuan volume
E. 3π satuan volume
Pembahasan:
Cara menghitung volume benda putar akan dikerjakan dengan metode kulit tabung. Di mana pada metode kulit tabung menggunakan partisi potongan benda putar yang sejajar dengan sumbu putar.
Sebelumnya, perlu untuk menentukan persamaan jari-jari putaran dan luas daerah yang diputar terlebih dahulu, Bentuk daerah luas dan benda putar yang dihasilkan terdapat pada gambar di bawah.

Menghitung volume benda putar:
V = 2π 0ʃ√2 x(2 ‒ x2) dx
V = 2π 0 ʃ√2 2x ‒ x3 dx
V = 2π[x2 ‒ 1/4x4 ]0√2
V = 2π[((√2)2 ‒ 1/4(√2)4) ‒ (02 ‒ 1/4·04)]
V = 2π[(2 ‒ 1/4 · 4) ‒ 0]
V = 2π(2 ‒ 1) = 2π
Jadi, volume benda putar yang terjadi jika daerah yang dibatasi oleh y = x2, garis y = 2, dan sumbu y diputar mengelilingi sumbu y sejauh 360o adalah 2π satuan volume.
Jawaban: C
Demikianlah tadi bagaimana dua bentuk rumus volume benda putar pada metode cakram dan kulit tabung. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
