Andi harus mengeluarkan uang Rp315.000,00 untuk membayar 3 buah barang A, 7 buah barang B, dan sebuah barang C, sedangkan Budi harus membayar Rp420.000,00 untuk 4 buah barang A, 10 buah barang B dan sebuah barang C. Jika Citra hanya membeli masing-masing sebuah dari ketiga jenis barang di atas, maka uang yang harus dibayarkan Citra adalah ….
(A) Rp100.000,00
(B) Rp105.000,00
(C) Rp110.000,00
(D) Rp125.000,00
(E) Rp150.000,00

Jawab: (B)

Misalkan harga barang A = A, harga barang B = B, dan harga barang C = C. Dari soal dapat dibentuk persamaan-persamaan berikut:

• Persamaan (i):
  Andi harus mengeluarkan uang Rp315.000,00 untuk membayar 3 buah barang A, 7 buah barang B, dan sebuah barang C → 3A + 7B + C = 315.000

• Persamaan (ii):
  Budi harus membayar Rp420.000,00 untuk 4 buah barang A, 10 buah barang B dan sebuah barang C → 3A + 7B + C = 315.000

Citra hanya membeli masing-masing sebuah dari ketiga jenis barang di atas. Sehingga uang yang harus dibayarkan Citra = A + B + C. Nilai A, B, dan C dapat diperoleh dengan menyelesaikan sistem persamaan linear tiga variabel (SPLTV) tersebut.

Pertama, eliminasi c dari persamaan (i) dan (ii):

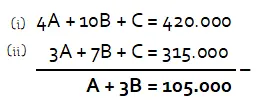
Selanjutnya, jumlahkan persamaan (i) dan persamaan (ii) sehingga akan diperoleh persamaan berikut.

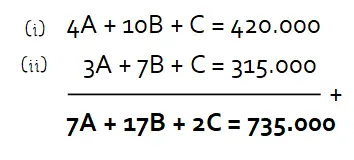
Diperoleh jumlah persamaan (i) dan (ii) adalah 7A + 17B + 2C = 735.000

Sehingga,

(2 + 5)A + (2 + 15)B + 2C = 735.000

2A + 5A + 2B + 15B + 2C = 735.000

2A + 2B + 2C + 5A + 15B = 735.000

2A + 2B + 2C + 5(A + 3B) = 735.000

Substitusi nilai A + 3B = 105.000 pada persamaan di atas sehingga dapat diperoleh persamaan berikut.

2A + 2B + 2C + 5×105.000 = 735.000

2A + 2B + 2C + 525.000 = 735.000

2A + 2B + 2C = 735.000 – 525.000

2(A + B + C) = 210.000

A + B + C = 105.000

Citra hanya membeli masing-masing sebuah barang. Jadi, uang yang harus dibayarkan Citra = A + B + C = Rp105.000,00.