Jika P(x) : (x2 + 2) sisanya 3x – 5 dan jika P(x) : (x2 + 4) sisanya 2x + 7. Berapakah sisa P(X) : (x^2 + 2)(x^2 + 4)?
Jawab:
Soal yang diberikan di atas dapat dikerjakan menggunakan teorema sisa yaitu untuk suku banyak f(x) berderajat n dibagi dengan (x – k) maka sisanya adalah S(x) = f(k).
- Diketahui:
- P(x) : (x2 + 2) → S(x) = 3x – 5
- P(x) : (x2 + 4)→ S(x) = 2x + 7
Bilangan pembuat nol pembagi P(x):
(x2 + 2) = 0
(x – (√–2))(x + (√–2)) = 0
x1 = i√2 atau x2 = –i√2
(x2 + 4) = 0
(x – (√–4))(x + (√–4)) = 0
x3 = 2i atau x4 = –2i
Misalkan sisa pembagian P(X) oleh (x^2 + 2)(x^2 + 4) adalah Ax + B sehingga P(x) = (x2 + 2)(x2 + 4) · H(x) + Ax + B. Berdasarkan teorema sisa dapat dibentuk dua persamaan berikut.
- f(i√2) = S(i√2)
0 + A(i√2) + B = 3(i√2) – 5
Ai√2 + B = 3i√2 – 5
- f(2i) = S(2i)
0 + A(2i) + B = 2(2i) + 7
2Ai + B = 4i + 7
Nilai A dan B dapat diketahui dengan menyelesaikan sistem persamaan linear dua variabel (SPLDV) untuk persamaan (i) Ai√2 + B = 3i√2 – 5 dan persamaan (ii) 2Ai + B = 4i + 7 seperti langkah penyelesaian berikut.
Menentukan nilai A:
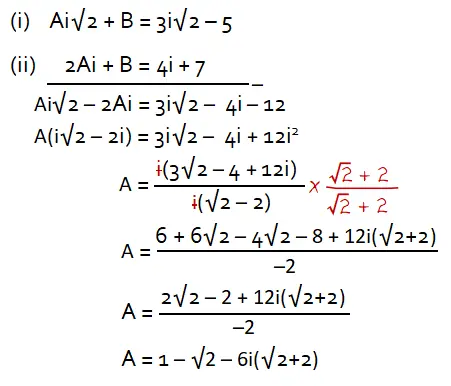
Menentukan nilai B:
2Ai + B = 4i + 7
2i(1 – √2 – 6i(√2+2)) + B = 4i + 7
2i – 2i√2 – 12i2(√2+2) + B = 4i + 7
2i – 2i√2 + 12(√2+2) + B = 4i + 7
2i – 2i√2 + 12√2 + 24 + B = 4i + 7
B = 4i – 2i + 2i√2 – 12√2 – 24 + 7
B = 2i + 2i√2 – 12√2 – 17
B = 2i + 2√2(i – 6) – 17
Jadi, jawaban untuk berapakah sisa P(X) : (x^2 + 2)(x^2 + 4) adalah S(x) = Ax + B = (1 – √2 – 6i(√2+2)) + 2i + 2√2(i – 6) – 17.