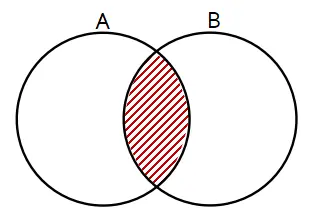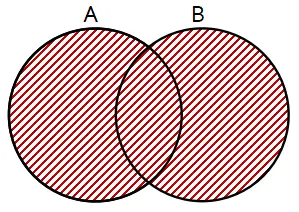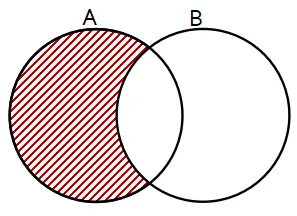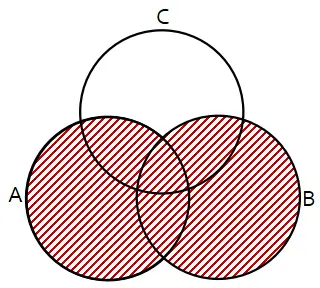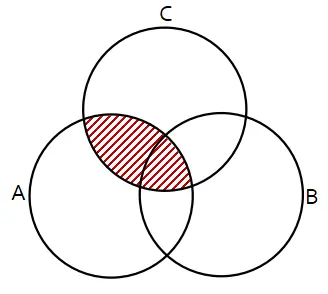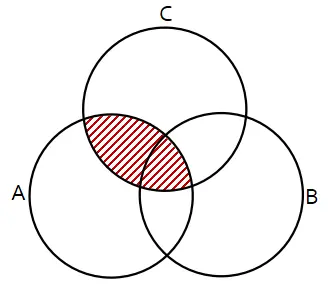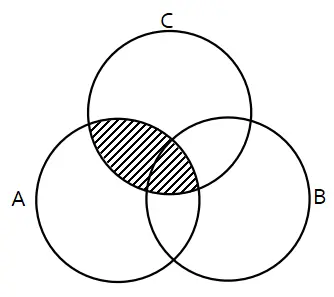
Daerah yang diarsir menyatakan ….
(A) (A ∩ B) ∪ (A ∩ C)
(B) (A ∪ B) ∩ (A ∩ C)
(C) (A ∪ B) ∩ (A ∪ C)
(D) (A ∪ C) ∩ (B ∪ C)
(E) (B – A) ∪ (C – A)

Jawab: (B)

Beberapa operasi himpunan terdiri dari irisan, gabungan, dan selisih. Bentuk diagram venn yang menyatakan operasi irisan, gabungan, dan selisih dua himpunan terdapat pada daerah arsiran berikut.

Irisan 2 himpunan:
A ∩ B = anggota himpunan yang terdapat pada himpunan A dan B.

Gabungan 2 himpunan:
A ∪ B = gabungan semua anggota himpunan A dan B.

Selisih 2 himpunan:
A – B = himpunan anggota A yang bukan anggota himpunan B.

Daerah yang diarsir pada soal merupakan seluruh anggota himpunan A serta anggota B dan C yang sama (B ∩ C).

Anggota himpunan (A ∪ B):

Anggota himpunan (A ∩ C):

Anggota himpunan (A ∪ B) ∩ (A ∩ C):

Jadi, daerah yang diarsir menyatakan (A ∪ B) ∩ (A ∩ C).