Perhatikan gambar!
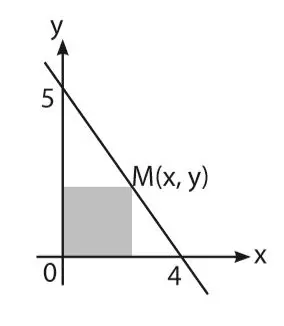
Luas daerah yang diarsir pada gambar akan mencapai maksimum jika koordinat titik M adalah ….
A. ( 2, 5)
B. ( 2, 5/2)
C. ( 2, 2/5)
D. (5/2, 2)
E. (2/5, 2)
Jawab: B
Titik M berada pada sebuah garis yang diketahui melalui dua titik yaitu (4, 0) dan (0, 5). Persamaan garis lurus tersebut dapat ditentukan dengan cara berikut.
Menentukan persamaan garis lurus:
5(x − 4) = −4y
5x − 20 = −4y
4y = 20 − 5x
y = 5 − 5/4x
Daerah yang diarsir berupa persegi panjang, sehingga luasnya dapat dihitung dengan rumus luas L = panjang (p) × lebar (l). Misalkan lebar persegi panjang = x dan lebarnya sama dengan y = 5 − 5/4x.
Persamaan luas persegi panjang:
L = x(5 − 5/4x)
L = 5x − 5/4x2
Luas daerah yang diarsir pada gambar akan mencapai maksimum saat turunan pertama persamaan luas sama dengan nol (L’ = 0).
Luas maksimum: L’ = 0
5x − 5/4x2 = 0
5 − 5/2x = 0
5/2x = 5
x = 5 : 5/2
x = 5 × 2/5 = 2
Luas maksimum dicapai saat titik absis x = 2. Substitusi nilai x pada persamaan y = 5 − 5/4x untuk mendapatkan nilai titik ordinat.
Menentukan titik ordinat (y):
y = 5 − 5/4x
y = 5 − 5/4(2)
y = 10/2 − 5/2 = 5/2
Diperoleh titik koordinat saat luas daerah yang diarsir maksimum yaitu x = 2 dan y = 5/2. Jadi, luas daerah yang diarsir pada gambar akan mencapai maksimum jika koordinat titik M adalah (2, 5/2).
Cara Cepat!!!
Luas daerah yang diarsir pada gambar akan mencapai maksimum saat absis titik M berada di setengah titik potong garis pada sumbu x dan ordinat titik M berada di setengah titik poting garis pada sumbu y.
Diketahui titik potong dengan sumbu x adalah 4 dan titik potong dengan sumbu y adalah 5. Koordinat titik M agar luas maksimum: M(1/2x, 1/2y) = M(1/2×4, 1/2×5) = M(2, 5/2).