UTBK 2019/PK

Pertidaksamaan dengan daerah yang diarsir sebagai representasi himpunan penyelesaiannya adalah ….

(A) 3x − 4y + 12 ≤ 0 

(B) 2x + 3y + 12 ≥ 0 

(C) 3x − 4y + 12 ≤ 0  

(D) 4x − 3y − 12 ≥ 0  

(E) 4x + 3y + 12 ≤ 0  

Jawab: (C)

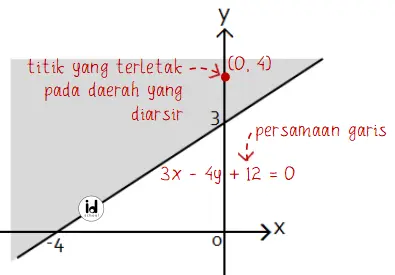
Daerah yang diarsir dibatasi oleh sebuah garis lurus yang belum diketahui persamaannya. Untuk mencari persamaan garis lurus terssebut, perhatikan dua titik yang dilalui oleh garis.

Diketahui ada dua titik yang dilalui garis lurus tersebut yaitu (–4, 0) dan (0, 3). Rumus persamaan garis lurus yang diketahui melalui dua titik:

Dua titik yang melalui garis lurus adalah (–4, 0) dan (0, 3) sehingga nilai x₁ = –4, x₂ = 0, y₁ = 0, dan y₂ = 3. Substitusi nilai-nilai tersebut pada rumus persamaan garis lurus untuk mendapatkan persamaan garis lurus tersebut.

Persamaan garis lurus  pada soal dapat dicari seperti langkah penyelesaian berikut.

4y = 3(x + 4)

4y = 3x + 12  

3x – 4y + 12 = 0

Diperoleh persamaan garis lurus pada soal adalah 3x – 4y + 12 = 0.

Selanjutnya adalah menentukan tanda pertidaksamaan yang digunakan. Pada gambar yang diberikan terdapat sebuah garis lurus yang tidak putus-putus. Artinya, tanda persamaan yang digunakan adalah lebih besar sama dengan (≥) atau lebih kecil sama dengan (≤).

Untuk menentukan tanda pertidaksamaan yang akan digunakan, ambil satu titik (sembarang) pada daerah yang diarsir. Misalnya ambil titik (0, 4).

Substitusi nilai absis (x) dan ordinat (y) dari titik (0, 4) ke persamaan garis yang diperoleh. Jika hasilnya negatif (kurang dari nol), pertidaksamaan menggunakan tanda ≤. Jika hasilnya positif (lebih dari nol), pertidaksamaan menggunakan tanda ≥.   

Hasil substitsui x = 0 dan y = 4 adalah 3x – 4y + 12 = 3(0) – 4(4) + 12 = 0 – 16 + 12 = –4. Nilai hasil perhitungannya adalah negatif (kurang dari nol). Sehingga tanda pertidaksamaan yang digunakan adalah ≤ (lebih kecil sama dengan).

Jadi, pertidaksamaan dengan daerah yang diarsir sebagai representasi himpunan penyelesaiannya adalah 3x − 4y + 12 ≤ 0.