Persamaan garis lurus disebut juga dengan persamaan linear karena hubungan matematis dari persamaan berupa garis lurus. Bentuk umum persamaan garis lurus dinyatakan dalam persamaan y = mx + c, dengan m adalah gradien, x merupakan variabel, dan c adalah konstanta. Persamaan garis lurus adalah suatu persamaan dua variabel dengan pangkat yang dapat membentuk garis lurus dengan kemiringan tertentu. Pangkat tertinggi dari variabel pada persamaan sebuah garis lurus adalah satu. Contoh persamaan untuk garis lurus adalah y = 2x, y = ‒1/2x, y = 2, 3x + 4y = 18, dan lain sebagainya.
Garis lurus merupakan kumpulan titik-titik dengan jumlah tak terhingga dan saling berdampingan. Sebuah garis lurus dapat dinyatakan dalam beberapa persamaan yang ekuivalen. Misalnya, diketahui sebuah garis lurus memiliki persamaan 2x ‒ y = 8 atau y = 2x ‒ 8. Kedua persamaan tersebut menghasilkan nilai dan memiliki bentuk grafik yang sama.
Baca Juga: Cara Menggambar Garis Lurus /Linear dari Suatu Persamaan
Bagaimana cara menentukan persamaan garis lurus? Apa bentuk rumus yang dapat digunakan untuk menentukan persamaan garis lurus? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Kemiringan (Gradien) Garis Lurus
- Posisi Antara Dua Garis
- Rumus Persamaan Garis Lurus
- Contoh Soal dan Pembahasan
Kemiringan (Gradien) Garis Lurus
Sebuah garis lurus dapat memiliki kemiringan tertentu dengan condong ke kanan atau condong ke kiri. Garis lurus juga dapat berupa garis horizontal (lurus mendatar) atau vertikal (lurus tegak atas/bawah). Besar kemiringan garis dapat dinyatakan melalui sebuah nilai yang disebut dengan gradien. Garis yang condong ke kanan memiliki nilai positif, sedangkan garis yang condong ke kiri memiliki nilai negatif. Besar nilai gradien adalah hasil perbandingan kemiringan garis untuk selisih nilai ke atas/bawah (sumbu y) dan ke kanan/kiri (sumbu x).
Simbol gradien dinyatakan dengan huruf m dengan nilai m sama dengan perbandingan banyaknya satuan pada sumbu y dan sumbu x atau m = Δy/Δx.
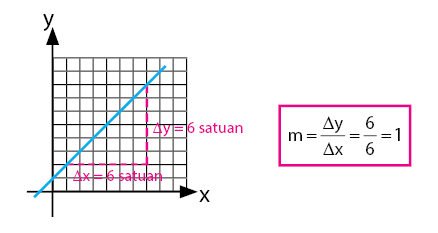
Cara menentukan nilai gradien disesuaikan dengan bentuk soalnya. Misalnya pada persamaan garis yang dinyatakan dalam bentuk y = mx + c. Nilai gradien garis pada bentuk persmaan garis tersebut sama dengan bilangan didepan variabel x yaitu m. Sebagai contoh diketahui persamaan garis lurus y = 2x + 5 maka nilai gradien garis tersebut adalah m = 2.
Pada persamaan garis lurus yang dinyatakan dalam bentuk ax + by = c nilai gradien dapat ditentukan dengan persamaan m = ‒a/b. Contoh pada persamaan garis lurus 3x + y = 5 memiliki nilai gradien m = ‒a/b = m = ‒3/1=m = ‒3.
Nilai gradien dari suatu garis lurus yang melalui dua titik yang diketahui dapat ditentukan melalui beberapa cara seperti berikut.
Baca Juga: Sudut Pusat dan Sudut Keliling pada Lingkaran
Posisi Antara Dua Garis
Garis lurus dapat dinyatakan dalam beberapa bentuk persamaan. Semua persamaan garis lurus mempunyai karakteristik yaitu memiliki pangkat tertinggi sama dengan 1. Contoh beberapa bentuk persamaan garis lurus dan grafiknya diberikan seperti berikut.
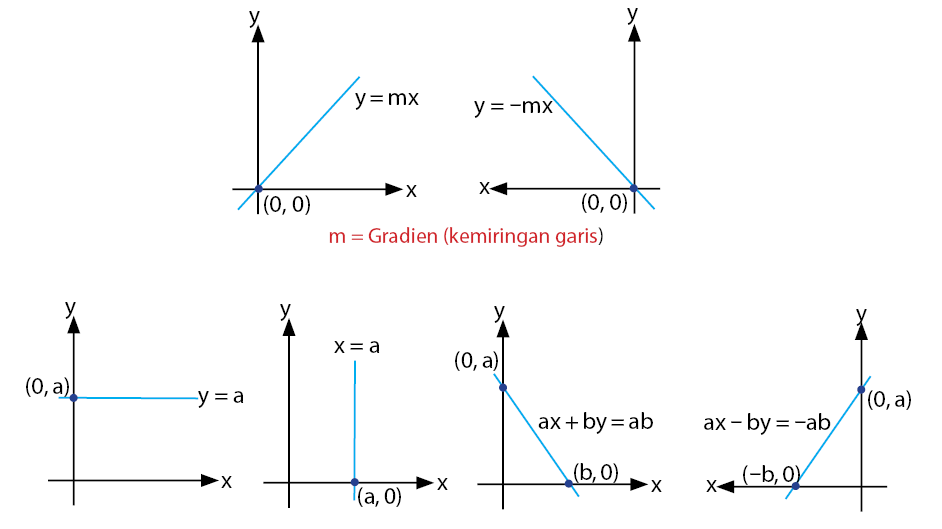
Dua buah garis dapat saling sejajar atau berpotongan tegak lurus. Kedua garis yang memiliki hubungan saling sejajar dan tegak lurus memiliki karakteristik pada nilai gradien. Nilai gradien pada dua garis yang saling sejajar adalah sama, sedangkan nilai gradien pada dua garis yang saling tegak lurus adalah lawan kebalikan.
Misalnya terdapat sebuah garis lurus pertama yang memiliki nilai gradien m1 = 2. Garis lurus kedua yang saling sejajar dengan garis pertama akan memiliki nilai gradien yang sama yaitu m2 = 2. Sedangkan garis lurus kedua yang saling tegak lurus dengan garis pertama memiliki nilai gradien lawan kebalikannya yaitu m2 = ‒1/2.
Keterangan:
- Garis sejajar merupakan dua buah garis yang tidak pernah akan mempunyai titik potong. Dua garis yang saling sejajar memiliki gradien yang sama.
- Dua garis yang saling tegak lurus mempunyai satu titik potong dan ruas garus membentuk sudut 90o. Dua garis yang saling tegak lurus memiliki gradien yang berlawan kebalikan.
Baca Juga: Operasi pada Bilangan Bulat
Rumus Persamaan Garis Lurus
Sebuah garis lurus dapat diketahui persamannya melalui rumus persamaan garis lurus dengan sedikit perhitungan. Ada dua bentuk rumus yang sering digunakan untuk menentukan persamaan garis lurus. Penggunaan kedua bentuk rumus dipilih berdasarkan apa informasi yang diberikan pada soal. Bentuk rumus persamaan garis lurus pertama digunakan untuk soal dengan keterangan sebuah gradien dan satu titik yang dilalui garis. Bentuk rumus yang kedua adalah soal menentukan persamaan garis lurus dengan keterangan dua buah titik yang dilalui.
Dua bentuk rumus persamaan dari garis lurus diberikan seperti persamaan di bawah.
Baca Juga: Kesebangunan dan Kekongruenan
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Aplikasi Gradien
Perhatikan gambar berikut!

Sebuah tangga bersandar pada dinding tembok (seperti pada gambar). Kemiringan tangga terhadap dinding tembok adalah ….
A. 4/3
B. 5/4
C. 4/5
D 3/4
Pembahasan:
Untuk menentukan kemiringan tangga tersebut, kita perlu mencari tinggi tembok terlebih dahulu. Gunakan teorema Pythagoras untuk mencari tinggi tembok (t).
t2 = 102 ‒ 62 = 100 ‒ 36
t2 = 64 → t = 8 m
Kemiringan dalam garis lurus merupakan gradien. Jadi, untuk mencari kemiringan tangga terhadap dinding tembok dapat diperoleh menggunakan rumus gradien.

Karena garis condong ke kanan, maka nilai gradiennya akan positif yaitu m = 8/6 = 4/3
Jawaban: A
Contoh 2 – Soal Aplikasi Gradien
Persamaan garis lurus yang bergradien 4 dan melalui titik (0, ‒7) adalah .…
A. y = 4x ‒ 7
B. y = 4x + 7
C. y = 1/4x ‒ 7
D. y = 1/4x ‒ 7
Pembahasan:
Bedasarkan keterangan yang diberikan pada soal dapat diperoleh informasi bahwa garis memiliki nilai gradien m = 4 dan melalui satu titik yaitu titik (0, ‒7). Sehingga rumus yang digunakan untuk menentukan persamaan garis lurus tersebut adalah y – y1 = m(x – x1). Cara menentukan persamaan garis lurus tersebut diberikan seperti langkah-langkah di bawah.

Jadi, persamaan garis lurus yang bergradien 4 dan melalui titik (0, ‒7) adalah y = 4x ‒ 7.
Jawaban: A
Baca Juga: Garis Lurus yang Saling Tegak Lurus
Contoh 3 – Soal Persamaan Garis Lurus
Persamaan garis yang melalui titik (‒1, 0) dan (3, ‒8) adalah .…
A. y = 2x + 2
B. y = 2x ‒ 2
C. y = ‒2x + 2
D. y = ‒2x ‒ 2
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi nilai x1 = ‒1, x2 = 3, y1 = 0, dan y2 = ‒8. Cara menentukan persamaan garis yang melalui dua titik dapat dilihat seperti langkah-langkah di bawah.

Jadi, persamaan garis yang melalui titik (‒1,0) dan (3, ‒8) adalah y = ‒2x ‒ 2.
Jawaban: D
Contoh 4 – Soal Persamaan Garis Lurus
Persamaan garis lurus yang sejajar dengan garis y =1/2x + 5 dan melalui titik P(‒1, 2) adalah ….
A. x + 2y ‒ 5 = 0
B. x ‒ 2y ‒ 5 = 0
C. x ‒ 2y + 5 = 0
D. x + 2y + 5 = 0
Pembahasan:
Diketahui persamaan garis y =1/2x + 5, sehingga nilai gradien garis y adalah m1 = 1/2. Karena persamaan garis baru yang akan dicari sejajar dengan garis y =1/2x + 5 maka m2 = m1 = 1/2.
Persamaan garis lurus yang sejajar dengan garis y =1/2x + 5 dan melalui titik P(‒1, 2):
y ‒ y1 = m2x ‒ x1
y ‒ 2 = 1/2 (x ‒ (‒1))
2( y ‒ 2 ) = x + 1
2y ‒ 4 = x + 1
x ‒ 2y + 5 = 0
Jadi, persamaan garis lurus yang sejajar dengan garis y =1/2x + 5 dan melalui titik P(‒1, 2) adalah x ‒ 2y + 5 = 0.
Jawaban: C
Sekian pembahasan mengenai cara menentukan persamaan garis lurus dan contoh soal serta pembahasannya. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Menentukan Persamaan pada 2 Garis Lurus yang Saling Sejajar





Obat insomnia gw😌