UTBK 2019/PK
Di dalam lingkaran besar terdapat dua lingkaran kecil identik yang saling bersinggungan di pusat lingkaran besar seperti pada gambar.

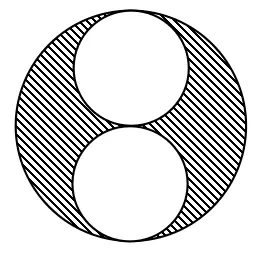
Kedua lingkaran kecil menyinggung lingkaran besar, jika jari-jari lingkaran kecil adalah 2 cm, maka luas daerah yang diarsir adalah ….
(A)  2π cm²
(B)  4π cm² 
(C)  8π cm²  
(D)  16π cm²  
(E)  18π cm² 

Jawab: (C)

• Dari soal dapat diketahui:
  • Panjang jari-jari lingkaran kecil: r = 2
  • Panjang jari-jari lingkaran besar: R = 2r = 2×2 = 4

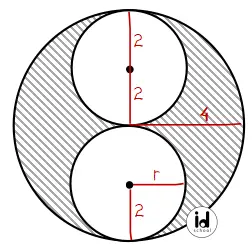
Luas daerah yang diarsir sama dengan selisih antara luas satu lingkaran besar dengan luas dua lingkaran kecil. Ingat! Rumus luas lingkaran adalah L = π×r² (r = jari-jari lingkaran).

Menghitung luas lingkaran besar:

L lingkaran besar = π×R²

L lingkaran besar = π×4² = 16π

Menghitung luas lingkaran kecil:

L lingkaran kecil = π×r²

L lingkaran kecil = π×2² = 4π

Luas daerah yang diarsir

= L lingkaran besar – 2×L lingkaran kecil

= 16π – 2×4π = 16π – 8π = 8π cm².

Jadi, luas daerah yang diarsir adalah 8π cm².