Rumus luas lingkaran yang memiliki panjang jari-jari r adalah L = π × r2. Sedangkan keliling lingkaran yang mempunyai panjang jari-jari r adalah K = 2π × r atau K = π × d (d = diamater). Contohnya, sebuah lingkaran memiliki panjang jari-jari 7 cm. Luas dan keliling lingkaran tersebut adalah L = 22/7 × 72 = 154 cm2 dan K = 22/7 × 14 = 44 cm.
Cara menghitung luas dan keliling lingkaran cukup mudah. Jika sudah tahu apa rumusnya. Rumus luas lingkaran cara menghitung dan contoh soalnya ada di bawah.
Daftar isi:
Bagian-Bagian Lingkaran
Lingkaran adalah salah satu jenis bangun datar sebuah bangun datar. Karakteristik lingkaran adalah memiliki titik pusat dan tepi lingkaran yang jaraknya sama. Contoh benda yang memiliki bentuk lingkaran adalah roda sepeda.
Jarak titik pusat ke tepi lingkaran sama dengan jari-jari (r). Jarak terjauh dari tepi ke tepi lingkaran sama dengan diameter (d).
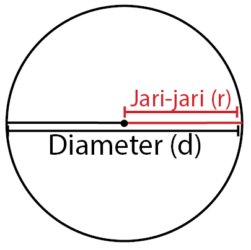
Sebuah lingkaran penuh, besar sudutnya adalah 360 derajat. Bagian lingkaran yang tidak penuh disebut juring lingkaran. Sementara sebagian tepi lingkaran disebut busur.
Rumus Lingkaran
Jari-jari dan diameter dibutuhkan untuk menghitung luas dan keliling lingkaran. Jadi pastikan sudah tahu nilai jari-jari atau diameter terlebih dahulu. Rumus luas dan keliling lingkaran ada di bawah.
1) Rumus keliling lingkaran
Keliling lingkaran sama dengan panjang bagian tepi yang membentuk bangun lingkaran. Bagian tepi yang membentuk bangun merupakan busur lingkaran. Panjang busur untuk satu lingkaran penuh sama dengan keliling lingkaran.
Perebandingan keliling lingkaran dan diameternya akan selalu sama. Nilai perbandingan keliling dan diameter sama dengan nilai

Rumus keliling:
K = 2 × π × r
atau
K = π × d
Keterangan:
π = 22/7 atau 3,14
d = diameter
r = jari-jari
Menggunakan nilai π = 22/7 saat jari-jari sama dengan 7 atau kelipatannya. Menggunakan nilai π = 3,14 saat jari-jari sama dengan 10 atau kelipatannya.
Cara menghitung keliling lingkaran
Soal:
Panjang jari-jari sebuah lingkaran adalah 7 cm. Tentukan kelilingnya!
Jawab:
Dari soal diketahui panjang jari-jari adalah r = 7 cm. Sehingga panjang diameternya adalah d = 14 cm.
Menghitung keliling:
K = π × d
K = 22/7 × 14 = 44 cm
Jadi, keliling lingkaran yang memilki jari-jari 7 cm adalah 44 cm.
2) Rumus Luas Lingkaran
Luas lingkaran adalah area yang dibatasi oleh tepi lingkaran. Rumus luas lingkaran yang memiliki jari-jari r adalah L = π × r2. Cara memperoleh rumus luas lingkaran ditunjukkan seperti cara berikut.
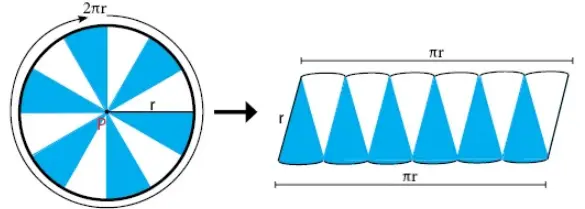
Sebuah lingkaran dipotong kecil-kecil seperti gambar di atas. Potongan tersebut disusun sehingga membentuk bangun persegi empat.
Barisan potongan juring warna biru memiliki panjang πr. Begitu juga untuk barisan potongan juring warna putih. Panjang potongan susunan juring-juring sama dengan panjang segi empat. Lebar segi empat sama dengan panjang jari-jari.
Luas bangun segi empat adalah panjang × lebar. Panjang persegi empat adalah πr dan lebarnya adalah r. Sehingga diperoleh rumus luas lingkaran yaitu L = πr × r = πr2.
Luas segi empat sama dengan luas lingkaran. Sehingga diperoleh rumus luas lingkaran adalah L = πr2 L = π × r × r.
Cara mengitung luas lingkaran
Soal:
Panjang jari-jari sebuah lingkaran adalah 7 cm. Tentukan luasnya!
Jawab:
Dari soal diketahui panjang jari-jari r = 7 cm sehingga,
Luas = π × r2 = 22/7 × 72
Luas = 22/7 × 7 × 7 = 154 cm2
Jadi, luas lingkaran yang memiliki jari-jari 7 cm adalah 154 cm2.
Baca Juga: Rumus Luas Trapesium +Contoh Soalnya
Contoh Soal dan Pembahasan
Contol soal mencari luas lingkaran dan kelilingnya ada di bawah. Selamat berlatih!
Contoh 1 – Luas bangun yang diarsir
Perhatikan gambar di bawah!
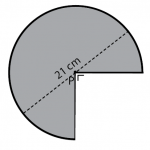
Luas bangun yang diarsir pada gambar di atas adalah …. (π = 22/7)
A. 86,625 cm2
B. 259,875 cm2
C. 346,500 cm2
D. 1.386 cm2
Pembahasan:
Bangun yang diarsir merupakan 3/4 lingkaran. Cara mencari luas bangun yang diarsir ada pada penyelesaian di bawah.
Jadi, luas bangun yang diarsir pada gambar di atas adalah 259,875 cm2.
Jawaban: B
Baca Juga: Cara Membandingkan Besar Nilai Pecahan
Contoh 2 – Keliling bangun tersebut adalah …
Perhatikan gambar di bawah!
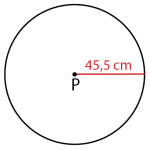
Keliling bangun tersebut adalah ….
A. 143 cm
B. 266 cm
C. 284 cm
D. 286 cm
Pembahasan:
Dari soal diketahui panjang jari-jari lingkaran adalah r = 45,5 cm. Sehingga, panjang diameternya adalah d = 91 cm.
Menghitung keliling:
K = π × d = 22/7 × 91
K = 22 × 91/7 = 286 cm
Jadi, keliling bangun tersebut adalah 286 cm.
Jawaban: D
Contoh 3 – Lintasan yang dilalui roda
Sebuah roda menggelinding sebanyak 20 kali. Jika panjang jari-jari roda itu 21 cm, panjang lintasan yang dilalui roda tersebut adalah ….
A. 132 cm
B. 260 cm
C. 1.320 cm
D. 2.640 cm
Pembahasan:
Dari soal diketahui jari-jari roda adalah r = 21 cm. Panjang lintasan yang dilalui roda untuk satu kali putaran sama dengan keliling lingkaran.
Menghitung keliling lingkaran:
K = 2 × π × r = 2 × 22/7 × 213
K = 2 × 22 × 3 = 132 cm
Jadi, panjang lintasan yang dilalui roda tersebut adalah 132 cm.
Jawaban: A
Contoh 4 – Luas roda
Sebuah roda dengan panjang garis tengah 1,4 m. Luas roda tersebut adalah ….
A. 3,08 m2
B. 1,54 m2
C. 0,77 m2
D. 0,39 m2
Pembahasan:
Diketahui dari soal bahwa panjang garis tengah roda = diameter 1,4 m. Sehingga panjang jari-jari roda adalah r = 1,4 : 2 = 0,7 cm.
Menghitung luas roda:
Luas = π × r2 = 22/7 × 0,70,1 × 0,7
Luas = 22 × 0,1 × 0,7 = 1,54 m2
Jadi, luas roda tersebut adalah 1,54 m2.
Jawaban: C
Demikianlah ulasan rumus luas dan keliling lingkaran. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
