Diketahui 6 siswa dan 3 siswi duduk berdiskusi mengelilingi meja bundar, maka peluang tidak ada siswi berdampingan adalah ….

Jawab: C

Diketahui 6 siswa dan 3 siswi duduk berdiskusi mengelilingi meja bundar. Banyak cara mengelilingi meja bundar dapat diketahui melalui perhitungan dengan rumus permutasi siklis.

Susunan yang dapat terjadi untuk 6 siswa dan 3 siswi mengelilingi meja bundar dapat dihitung dengan rumus permutasi siklis seperti yang dilakukan pada cara berikut.

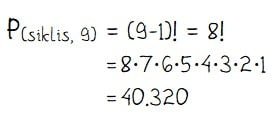
Kejadian untuk banyak susunan untuk tidak ada siswi berdampingan terdapat saat 3 siswi berada di antara 6 siswa. Cara 6 siswa menempati meja bundar dapat dihitung dengan permutasi siklis P(siklis, 6) = (6 ‒ 1)! = 5!

Sedangkan cara 3 siswi menempati meja bundar sama dengan banyak cara menempati enam posisi diantara dua siswa. Sehingga banyak cara 3 siswi untuk tidak berdampingan dapat dihitung dengan rumus permutasi 3 obyek dari 6 obyek (₆P₃).

Perhitungan banyak susunan yang dapat terjadi untuk tidak ada siswi berdampingan dapat dilakukan seperti cara berikut.

Peluang tidak ada siswi berdampingan saat mengelilingi meja bundar

= ^{banyak kejadian}/_{ruang sampel} 

= ^14.400/_40.320 

= ⁵/₁₄

Jadi, peluang tidak ada siswi berdampingan adalah ⁵/₁₄