UTBK 2023
Diketahui a + 2b − c = 2020, a − b = 2, serta a + c = 2018. Maka a² − b² = …
(A) 4.032
(B) 4.034
(C) 4.036
(D) 4.038
(E) 4.040

Jawab: (D)

Dari soal diketahui tiga persamaan yaitu,

• (i) a + 2b − c = 2020
• (ii) a − b = 2
• (iii)  a + c = 2018

Terdapat tiga persamaan dengan tiga variabel yaitu a, b, dan c. Nilai ketiga variabel tersebut dapat dicari tahu dengan menyelesaikan sistem persamaan linear.

1) Eliminasi b dari persamaan (i) dan (ii) dengan cara berikut.

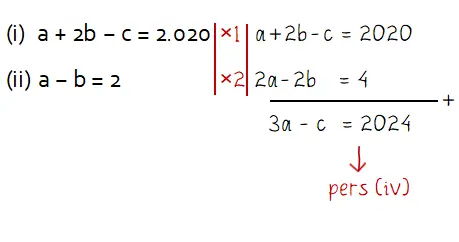
2) Eliminasi c dari persamaan (iii) dan (iv) untuk mendapatkan nilai a:

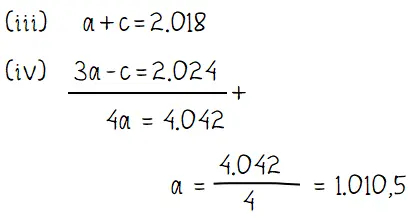
3) Menentukan nilai b: 
substitusi nilai a = 1.010,5 pada persamaan a − b = 2 untuk mendapatkan nilai b.

1.010,5 − b = 2

−b = 2 − 1.010,5

−b = −1.008,5  

b = 1.008,5  

4) Menghitung nilai a² − b²:

a² − b² = (a − b)(a + b)

= (1.010,5 − 1.008,5)(1.010,5 + 1.008,5)  

= 2×2.019 = 4.038

Maka a² − b² = 4.038 (D)