Dari suatu barisan aritmetika, diketahui suku ketiga adalah 36 dan jumlah suku kelima dan ketujuh

Dari suatu barisan aritmetika, diketahui suku ketiga adalah 36 dan jumlah suku kelima dan ketujuh adalah 144.

Jumlah sepuluh suku pertama deret tersebut adalah ….
A. 840
B. 660
C. 640
D. 630
E. 315

Jawab: B

Dari soal diketahui suku ketiga adalah 36 dan jumlah suku kelima adalah 144 dari suatu barisan aritmatika sehingga dapat dibentuk dua persamaan berikut.

Persamaan (i): suku ketiga = 36
U₃ = 36
a + 2b = 36

Persamaan (ii): suku kelima + suku ketujuh = 144
U₅ + U₇ = 144
a + 4b + a + 6b = 144
2a + 10b = 144
a + 5b = 72

Diperoleh dua persamaan yaitu (i) a + 2b = 36 dan (ii) a + 5b = 72. Nilai a dan b dapat dicari tahu dengan metode eliminasi atau substitusi dari suatu SPLDV.

Menentukan nilai b:
Eliminasi a dari persamaan (i) dan (ii) untuk mendapatkan nilai b.

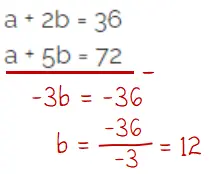
Menentukan nilai a: substitusi nilai b = 12 pada persamaan (i)

a + 2×12 = 36
a + 24 = 36
a = 36 − 24 = 12

Menghitung jumlah sepuluh suku pertama deret geometri tersebut:
S_n = ⁿ/₂(2a + (n − 1)b)
S₁₀ = ¹⁰/₂(2×12 + 9×12)
S₁₀ = 5 × (24 + 108)
S₁₀ = 5 × 132 = 660

Jadi, jumlah sepuluh suku pertama deret tersebut adalah 660.