UTBK 2023/PM
Dua buah pasir A dan B dituangkan secara terpisah membentuk kerucut. Radius alas kerucut pasir A selalu sama dengan tingginya dan radius alas kerucut pasir B selalu dua kali tingginya.

Diketahui P₁ adalah pusat alas tumpukan pasir A dan P₂ adalah pusat alas tumpukan pasir B. Jarak P₁ dan P₂ adalah 10 cm.

Soal 1

Jika kedua jenis pasir tersebut dituangkan dengan laju volume yang sama maka r₁ : r₂ = ….
(A)   1 : ³√2
(B)   ³√2 : 1
(C)   1 : √2
(D)   √2 : 1
(E)   1 : √3

Jawab: (A)

Dua buah pasir A dan B dituangkan secara terpisah membentuk kerucut. Misalkan jari-jari kerucut A adalah r₁ dan tinggi kerucut A adalah h₁. Sedangkan jari-jari kerucut B adalah r₂ dan tinggi kerucut B adalah h₂.

Dari keterangan pada soal dapat diketahui beberapa informasi seperti berikut.

• Radius alas kerucut pasir A selalu sama dengan tingginya: r₁ = h₁
• Radius alas kerucut pasir B selalu dua kali tingginya: r₂ = 2h₂, sehingga h₂ = ¹/₂r₂

Rumus volume kerucut:

• Keterangan:
  • V = volume kerucut
  • π = ²²/₇ atau π = 3,14
  • r = jari-jari alas kerucut
  • t = tinggi kerucut

Diketahui bahwa kedua jenis pasir tersebut dituangkan dengan laju volume yang sama. Dari keterangan tersebut, untuk setiap waktu t yang sama maka besar volume pasir A sama dengan volume pasir B.

Sehingga pada waktu t yang sama dapat membentuk persamaan berikut.

V_A = V_B

¹/₃ × π × r₁² × h₁ = ¹/₃ × π × r₂² × h₂

¹/₃ × π × r₁² × r₁ = ¹/₃ × π × r₂² × (¹/₂r₂)

r₁³ = ¹/₂ × r₂³

Dengan demikian, jika kedua jenis pasir tersebut dituangkan dengan laju volume yang sama maka r₁ : r₂ = 1 : ³√2

Soal 2

Jika kedua jenis pasir dituangkan dengan laju volume yang sama maka h₁ : h₂ = ….

(A) 2³√2 : 1

(B) ³√4 : 1

(C) √2 : 2

(D) 2 : ³√4

(E) 2³√2 : 1

Jawab: (B)

Dua buah pasir A dan B dituangkan secara terpisah membentuk kerucut. Misalkan jari-jari kerucut A adalah r₁ dan tinggi kerucut A adalah h₁. Sedangkan jari-jari kerucut B adalah r₂ dan tinggi kerucut B adalah h₂.

Dari keterangan pada soal dapat diketahui beberapa informasi seperti berikut.

• Radius alas kerucut pasir A selalu sama dengan tingginya: r₁ = h₁
• Radius alas kerucut pasir B selalu dua kali tingginya: r₂ = 2h₂, sehingga h₂ = ¹/₂r₂

Menentukan perbandingan tinggi kedua kerucut:

Dengan demikian, jika kedua jenis pasir dituangkan dengan laju volume yang sama maka h₁ : h₂ = ³√4 : 1 (B).

Soal 3

Kedua jenis pasir terus dituangkan dengan laju yang sama hingga kedua dasarnya bertemu di satu titik. Jarak antara P₁ dengan titik temu adalah ….

Jawab: (D)

Dari perhitungan yang dilakukan pada pembahasan soal 1 dapat diperoleh perbandingan jari-jari r₁ : r₂ = 1 : ³√2. Sehingga dapat disimpulkan bahwa r₂ = ³√2r₁.

Keterangan pada soal menyatakan bahwa jarak antara P₁ dan P₂ sama dengan 10 cm. Saat kedua alas kerucut bertemu maka memenuhi persamaan r₁ + r₂ = 10. Substitusi persamaan r₂ = ³√2r₁ ke persamaan tersebut untuk mendapatkan nilai r₁ seperti yang dilakukan pada langkah penyelesaian berikut.

Menentukan jarak antara P₁ dengan titik temu (r₁):

r₁ + r₂ = 10

r₁ + ³√2r₁ = 10

r₁(1 + ³√2) = 10

Jadi, jarak antara P₁ dengan titik temu adalah r₁ = ¹⁰/_{1 + ³√2} cm.

Soal 4

Jika kedua jenis pasir tersebut dituangkan dengan laju volume yang sama dan diketahui h₂ = 1 m (tinggi kerucut tumpukan pasir kedua), jarak antara kedua puncak tumpukan pasir adalah ….

(A) √109

(B) √101

(C) √(101 − 2³√4 + ³√16)

(D) √(101 + 2³√4 + ³√16)

(E) √(101 − 2³√4 + ³√4)

Jawab: (C)

Diketahui nilai h₂ = 1 m dan dipeorleh hasil perhitungan soal nomor 2 yaitu perbandingan h₁ : h₂ = ³√4 : 1. Sehingga h₁ dapat dicari tahu dengan cara berikut.

Pada kerucut A, radius alas kerucut selalu sama dengan tinggi kerucut sehingga r₁ = h₁ = ³√4 cm.

Jarak antara kedua puncak tumpukan pasir sama dengan panjang garis AB pada gambar di bawah.

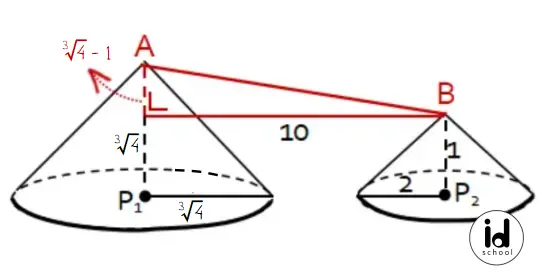
Panjang AB dapat dihitung menggunakan Teorema Pythgoras seperti yang dilakukan pada cara berikut.

Menghitung panjang AB:

AB² = 10² + (³√4 − 1)² 

AB² = 100 + (³√16 − 2³√4 + 1)

AB² = 100 + ³√16 − 2³√4 + 1

AB² = 101 − 2³√4 + ³√16

AB = √(101 − 2³√4 + ³√16)

Jadi, jarak antara kedua puncak tumpukan pasir sama dengan (C) AB = √(101 − 2³√4 + ³√16).