Dua jenis pasir yakni pasir A dan B dituangkan secara terpisah hingga membentuk kerucut. Radius alas kerucut A sama dengan setengah tingginya, sedangkan radius pasir B sama dengan tiga kali tingginya.
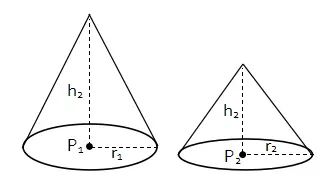
P1 adalah pusat alas tumpukan pasir A dan P2 adalah pusat alas tumpukan pasir B. Jarak antara P1 dan P2 adalah 10 cm.
Pertanyaan:
Soal 1
Jika kedua jenis pasir tersebut dituangkan dengan laju volume yang sama maka r1 : r2 = ….
(A) 1 : 3√6
(B) 3√6 : 1
(C) 1 : √6
(D) √6 : 1
(E) 1 : √3
Jawab: (A)
Dua jenis pasir yakni pasir A dan B dituangkan secara terpisah hingga membentuk kerucut. Misalkan jari-jari kerucut A adalah r1 dan tinggi kerucut A adalah h1. Sedangkan jari-jari kerucut B adalah r2 dan tinggi kerucut B adalah h2.
Dari keterangan pada soal dapat diketahui beberapa informasi seperti berikut.
- Radius alas kerucut A sama dengan setengah tingginya: r1 = 1/2h1 sehingga h1 = 2r1
- Radius alas kerucut B sama dengan tiga kali tingginya: r2 = 3h2 sehingga h2 = 1/3r2
Rumus volume kerucut:
V = 1/3 × π × r2 × t
Keterangan:
V = volume kerucut
π = 22/7 atau π = 3,14
r = jari-jari alas kerucut
t = tinggi kerucut
Diketahui bahwa kedua jenis pasir tersebut dituangkan dengan laju volume yang sama. Maka untuk setiap waktu t yang sama memiliki besar volume pasir yang sama.
Sehingga ntuk setiap t waktu akan memenuhi persamaan berikut.
VA = VB
1/3×π×(r1)2×(2r1) = 1/3×π×(r2)2×(1/3r2) 1/3×π ×r12×2r1 = 1/3×π×r22×1/3r2
2r13 = 1/3r23
6r13 = r23
Jadi, jika kedua jenis pasir tersebut dituangkan dengan laju volume yang sama maka r1 : r2 = 1 : 3√6.
Soal 2
Jika kedua jenis pasir dituangkan dengan laju volume yang sama maka h1 : h2 = ….
(A) 1 : 3√62
(B) 3√62 : 1
(C) 1 : √6
(D) √6 : 1
(E) 1 : √3
Jawab: (B)
Dua jenis pasir yakni pasir A dan B dituangkan secara terpisah hingga membentuk kerucut. Misalkan jari-jari kerucut A adalah r1 dan tinggi kerucut A adalah h1. Sedangkan jari-jari kerucut B adalah r2 dan tinggi kerucut B adalah h2.
Dari keterangan pada soal dapat diketahui beberapa informasi seperti berikut.
- Radius alas kerucut A sama dengan setengah tingginya: r1 = 1/2h1 sehingga h1 = 2r1
- Radius alas kerucut B sama dengan tiga kali tingginya: r2 = 3h2 sehingga h2 = 1/3r2
Dari perhitungan sebelumnya dapat diketahui bahwa perbandingan jari-jari kedua kerucut pada soal nomor 1 diperoleh hasil r1 : r2 = 1 : 3√6.
Menentukan perbandingan tinggi kedua kerucut:
Jadi, jika kedua jenis pasir dituangkan dengan laju volume yang sama maka h1 : h2 = 3√62 : 1 (A).