Hasil ʃ
2x+3
√(3x2 + 9x – 1)
dx = ….
A. 2√(3x2 + 9x – 6)
B. 1/3√(3x2 + 9x – 6)
C. 2/3√(3x2 + 9x – 6)
D. 1/2√(3x2 + 9x – 6)
E. 3/2√(3x2 + 9x – 6)
Jawab: C
Hasil integral dapat dikerjakan dengan rumus integral substitusi yaitu ʃ f(g(x)) ∙ g'(x) dx = ʃ f(u) du. Pengerjaan menggunakan integral substitusi karena 2x+3 merupakan bagian dari turunan pertama 3x2 + 9x – 1.
Pertama, perlu untuk memisalkan fungsi 3x2 + 9x – 1 sebagai u terlebih dahulu.
Misal: u = 3x2 + 9x – 1
du = 6x + 9 dx
du = 3(2x + 3) dx
dx =
du3(2x+3)Selanjunya, substitusi u dan dx pada persamaan untuk menentukan hasil ʃ (2x+3)/(√(3×2 + 9x – 1) dx. Langkah penyelesaian hasil integral tersebut dilakukan seperti cara berikut.
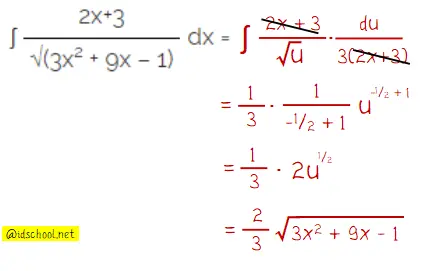
Jadi, hasil ʃ (2x+3)/(√(3×2 + 9x – 1) dx = 2/3√(3x2 + 9x – 6)