Ragam soal integral yang perlu diselesaikan cukup beragam. Untuk itu, sobat idschool perlu mengenali metode yang tepat untuk menyelesaikan soal integral. Ada dua bentuk soal integral yang biasanya dapat diselesaikan dengan rumus integral substitusi dan rumus integral parsial. Penggunaan rumus integral yang tepat menjadi kunci untuk mengerjakan/menentukan hasil integral suatu fungsi.
Rumus integral substitusi digunakan ketika bagian dari sebuah fungsi merupakan turunan dari fungsi lainnya. Biasanya, soal integral yang dapat diselesaikan menggunakan cara substitusi terdiri dari 2 faktor, di mana turunan dari salah satu faktornya memiliki hubungan dengan faktor lainnya.
Rumus integral parsial digunakan untuk soal integral yang biasanya terlihat cukup rumit/kompleks. Biasanya, cara ini digunakan ketika rumus integarl subsitusi tidak bisa digunakan. Soal integral yang dapat diselesaikan menggunakan integral pasrsial terbagi menjadi dua yaitu fungsi u dan dv.
Bagaimana bentuk rumus integral substitusi dan rumus integral parsial? Bagaimana bentuk soal yang dapat dikerjakan dengan rumus integral substitusi? Dan bagaimana bentuk soal yang dapat dikerjakan dengan rumus integral parsial? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Rumus Integral Substitusi
Pada bagian awal sudah disinggung sedikit tentang ciri-ciri soal integral yang dapat diselesaikan menggunakan rumus integral substitusi. Intinya, ciri-ciri soal integral yang dapat diselesaikan menggunakan rumus integral substitusi mempunyai faktor yang merupakan turunan dari faktor lainnya.
Perhatikan salah satu contoh soal integral yang dapat diselesaikan menggunakan rumus integral substitusi di bawah.
Pengerjaan soal integral seperti di atas membutuhkan teknik dan metode yang tepat untuk mendapatkan hasil integralnya. Metode yang tepat untuk menyelesaikan soal integral di atas adalah rumus integral substitusi. Sebelum mempelejarai cara menyelesaikan soal integral di atas, simak terlebih dahulu persamaan integral substitusi.
Rumus integral substitusi diberikan melalui persamaan di bawah.
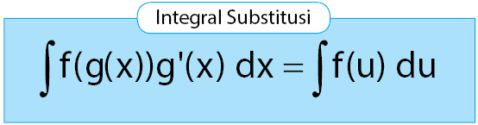
Sekarang, mari kita coba selesaikan soal integral yang telah diberikan sebelumnya menggunakan persamaan di atas. Perhatikan proses perngerjaan yang diberikan di bawah.
Perhatikan kembali soal integral yang diberikan!

Turunan dari x2 ‒ 4 adalah 2x,
dengan demikian, sobat idschool dapat menduga bahwa soal integral di atas dapat diselesaikan menggunakan rumus integral substitusi.
Perhatikan langkah-langkah untuk menggunakan rumus integral substitusi seperti pada cara berikut.
Misalkan:
u = x2 ‒ 4
du/dx = 2x → dx = du/2x
Sehingga, penyelesaian bentuk soal dengan menggunakan rumus integral substitusi dapat dilakukan seperti cara berikut.
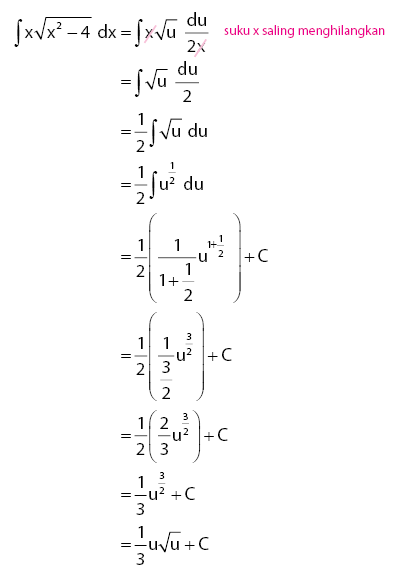
Setelah mendapatkan hasil akhir dalam persamaan u, sobat idschool perlu mengembalikan kembali pemisalan u = x2 ‒ 4 yang dilakukan di awal. Sehingga, dapat diperoleh hasil seperti berikut.
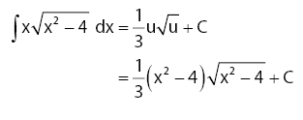
Baca Juga: Rumus Cepat Mengerjakan Soal Limit Tak Hingga pada Beberapa Bentuk Soal
Rumus Integral Parsial
Sebelumnya, telah disampaikan sekilas bahwa rumus integral parsial digunakan ketika tidak ada metode lain yang dapat digunakan untuk menyelesaikan soal integral yang diberikan. Cara ini bisa dibilang cara pamungkas yang dapat digunakan untuk menyelesaikan soal integral.
Contoh soal integral yang dapat diselesaikan dengan rumus integral parsial adalah sebagai berikut.

Soal integral yang diberikan di atas tidak dapat dikerjakan dengan rumus integral biasa. Metode substitusi juga tidak dapat mejadi solusi untuk menemukan hasil integral dari soal yang diberikan di atas. Sehingga, metode yang tepat untuk menyelesaikan soal integral yang diberikan di atas adalah rumus integral parsial. Sebelumnya, simak terlebih dahulu persamaan integral parsial berikut.
Secara umum, rumus integral persial dinyatakan melalui persamaan di bawah.

Selanjutnya, kita akan menyelesaikan soal integral yang diberikan sebelumnya menggunakan persamaan integral parsial di atas. Perhatikan proses pengerjaan yang akan diberikan di bawah.
Perhatikan kembali soal integral yang diberikan!
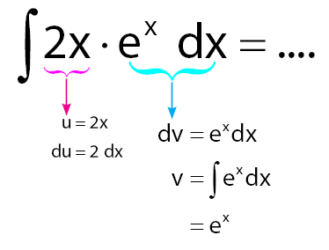
Selanjutnya, gunakan rumus integral parsial. Sehingga diperoleh persamaan di bawah.
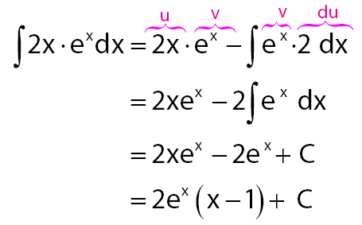
Sebenarnya, langkah-langkah di atas sudah cukup untuk menemukan hasil integral suatu fungsi. Namun, untuk beberapa kasus soal integral, cara di atas bisa menjadi membutuhkan usaha dan waktu yang lebih. Sehingga, ada rumus cepet untuk mengerjakan soal integral parsial. Berikut ini akan diuraikan cara cepat menentukan hasil integral parsial.
Proses pengerjaan integral parsial dengan cara cepat akan menggunakan soal yang sama seperti di atas, sehingga sobat idschool dapat membandingkan hasilnya.
Langkah awal sama seperti pengerjaan integral parsial dengan cara runut, yaitu memisal komponen menjadi u dan dv. Selanjutnya, sobat idschool perlu menurunkan u sampai hasil turunannya adalah 0 dan mengintegralkan dv sampai proses mengikuti u seperti yang ditunjukkan pada tabel di bawha.
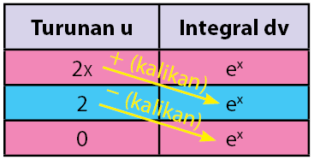
Hasil integral diperoleh dari perkalian dengan aturan seperti yang ditunjukkan anak panah. Sehingga, hasil integralnya dapat diperoleh seperti cara dan hasil berikut.
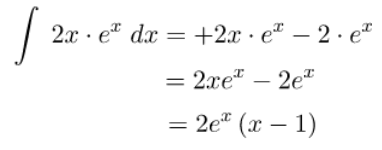
Selesai, demikianlah proses pengerjaan soal integral menggunakan rumus integral parsial. Bagaimana? Mudah Bukan?
Sekian pembahasan mengenai rumus integral substitusi dan rumus integral parsial. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Rumus Dasar Integral

