Himpunan penyelesaian pertidaksamaan
(A) {x ∊ R | x < 3/5}
(B) {x ∊ R | x < 5/3}
(C) {x ∊ R | x > 3/5}
(D) {x ∊ R | 3/5 < X < 1}
(E) {x ∊ R | x < 3/5 atau x > 1}
Jawab: (E)
Himpunan penyelesaian pertidaksamaan 2x/1-x < 3 adalah semua nilai x yang memenuhi pertidaksamaan tersebut. Cara menentukan himpunan penyelesaian pertidaksamaan 2x/1-x < 3 meliputi beberapa langkah berikut.
Langkah pertama, sederhanakan bentuk pertidaksamaan pecahan sehingga ruas kiri adalah nol. Caranya dengan mengurangi kedua ruas dengan bilangan 3 seperti penyelesaian berikut.
Samakan penyebutnya,
Sehingga:
Harga nol untuk pembilang:
5x − 3 = 0
5x = 3
x = 3/5
Harga nol untuk penyebut:
1 − x = 0
x = 1
Diperoleh dua nilai x dari harga nol pembilang dan penyebut yaitu x1 = 3/5 dan x2 = 1. Dua nilai x tersebut akan membagi garis bilangan menjadi tiga daerah yaitu daerah di kiri x = 3/5; antara titik x = 3/5 dan x = 1; serta di kanan titik x = 1 seperti gambar berikut.
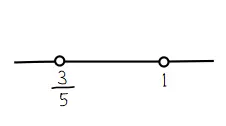
Perlu diketahui daerah mana yang menjadi Himpunan penyelesaian pertidaksamaan 2x/1-x < 3. Caranya dengan melihat nilai-nilai pada ketiga daerah tersebut.
Lakukan uji titik untuk mengetahui nilai-nilai yang dihasilkan oleh ketiga daerah tersebut. Misalkan ambil titik x = 0 (terletak di kiri x = 3/5 ). Substitusi x = 1 pada pertidaksamaan untuk mengetahui nilai positif/negatif yang dihasilkan.
Diperoleh hasil −3, sehingga dapat disimpulkan bahwa daerah di kiri x = 3/5 selalu bernilai negatif. Untuk dua daerah lainnya memiliki tanda yang berlainan sesuai urutan dari kiri. Sehingga daerah antara titik x = 3/5 dan x = 1 selalu bernilai positif dan daerah di kanan titik x = 1 selalu bernilai negatif.
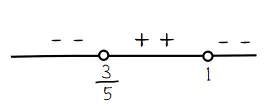
Pertidaksamaan memiliki bentuk kurang dari (<) sehingga himpunan penyelesaian dari pertidaksamaan tersebut adalah daerah dengan nilai-nilai negatif. Semua daerah negatif terletak di kiri x = 3/5 dan x = 1.
Gambar daerah yang menjadi himpunan penyelesaian dibuat seperti berikut.
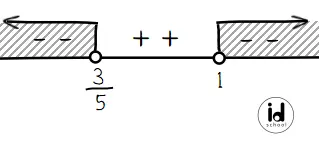
Jadi, himpunan penyelesaian pertidaksamaan 2x/1-x < 3 adalah {x ∊ R | x < 3/5 atau x > 1} (E).