Diketahui panjang rusuk kubus adalah 10 cm. Titik P dan titik Q berturut-turut merupakan titik tengah dari rusuk AB dan BC.
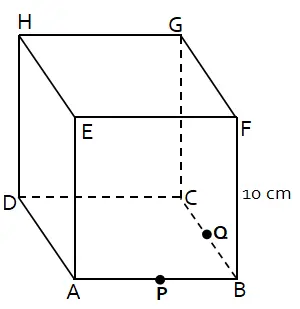
Jarak garis PQ ke garis EG adalah ….
Jawab: E
Jarak garis ke garis (jarak antara 2 garis) adalah panjang ruas garis yang menghubungkan dua garis tersebut. Di mana ruas garis tersebut tegak lurus dengan garis pertama dan kedua.
Cara yang perlu dilakukan adalah mengambil sebuah titik yang merupakan bagian dari garis pertama. Kemudian, proyeksikan titik tersbut pada garis ke dua. Selanjutnya dapat diperoleh ruas garis yang tegak lurus dengan kedua garis tersebut.
Sehingga jarak garis PQ ke garis EG sama dengan panjang ruas garis yang tegak lurus dengan kedua garis tersbeut, yaitu garis MN pada gambar berikut.
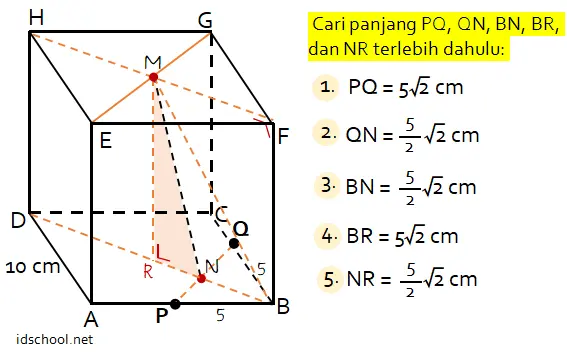
Jarak garis PQ ke garis EG adalah panjang ruas garis MN. Ruas garis tersebut merupakan sisi miring dari segitiga MNR yang dapat dihitung dengan rumus Pythagoras.
Sebelumnya perlu mencari panjang PQ, QN, BN, BR, dan NR terlebih dahulu. Panjang PQ, QN, BN, dan BR dapat dihitung dengan rumus Pythagoras. Sementara panjang NR sama dengan selilisih BR dan BN.
- PQ = 5√2 cm, sisi miring segitiga siku-siku sama kaki PBQ
- QN = 1/2PQ
QN = 1/2×5 = 5/2√2 cm
- 1/2×BN×PQ = 1/2×PB×BQ
BN × 5√2 = 5 × 5
BN = 25/5√2 = 5/2√2 cm
- NR = BR − BN
NR = 5√2 − 5/2√2 = 5/2√2 cm
Jarak garis PQ ke garis EG adalah panjang ruas garis MN. Cara menghitung panjang ruas garis MN dilakukan seperti langkah penyelesaian berikut.
Menghitung panjang MN:
MN2 = MR2 + RN2
MN2 = 102 + (5/2√2)2
MN2 = 100 + 50/4
MN2 = 100/4 + 50/4 = 150/4
MN = √150/4 = √(25×6)/√4
MN = 5√6/2 = 5/2√6 cm
Jadi, jarak garis PQ ke garis EG adalah 5/2√6 cm