Jarak garis ke garis atau jarak antara 2 garis adalah panjang ruas garis yang menghubungkan dua garis tersebut. Di mana ruas garis tersebut tegak lurus dengan garis pertama dan kedua. Pada dua garis yang berpotongan sama dengan nol (0), tidak memiliki jarak. Sedangkan jarak dua garis sejajar sama dengan panjang ruas garis terpendek yang menghubungkan kedua garis tersbebut.
Bagaimana cara menghitung jarak garis ke garis? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar isi:
Kedudukan 2 Garis pada Kubus
Dua buah ruas garis pada suatu bangun ruang memiliki 3 kedudukan yaitu sejajar, berpotongan, atau bersilangan.
Dua buah dikatakan saling sejajar jika kedua garis tersebut tidak memiliki titik potong. Pada sebuah kubus, dua buah garis sejajar terletak pada satu bidang yang sama.
Untuk dua garis dikatakan berpotongan jika memiliki satu buah titik potong. Sedangkan garis bersilangan pada suatu kubus terletak pada bidang yang berbeda sehingga, tidak sejajar dan tidak memiliki titik potong.
Gambaran 3 kedudukan dua garis pada kubus sesuai dengan kondisi berikut.

Baca Juga: Jarak Garis ke Bidang
Jarak Garis ke Garis
Jarak garis ke garis (jarak antara 2 garis) adalah panjang ruas garis yang menghubungkan dua garis tersebut. Di mana ruas garis tersebut tegak lurus dengan garis pertama dan kedua.
Cara yang dilakukan untuk menghitung jarak garis ke gatis adalah dengan mengambil sebuah titik yang merupakan bagian dari garis pertama. Proyeksikan titik tersebut pada garis ke dua.
Selanjutnya dapat diperoleh ruas garis yang tegak lurus dengan kedua garis tersebut. Garis tersebut merupakan jarak garis ke garis untuk kedua garis tersebut.
Pada dua garis yang berpotongan tidak memiliki jarak atau jarak garis ke garis sama dengan 0 (nol).
Untuk garis g sejajar dengan garis h. Sebuah garis ℓ tegak lurus dengan garis g dan garis h. Jarak garis g dan garis h sama dengan panjang ruang garis ℓ.

Pada dua garis yang bersilangan, jarak garis ke garis sama dengan jarak bidang yang memuat masing-masing garis. Atau jarak dua garis bersilangan sama dengan jarak terpendek dari satu garis ke bidang yang memuat garis lain.
Penentuan jarak garis ke garis yang saling besilangan disesuaikan dengan kedudukan dari dua garis.
Sebagai contoh, garis g dan garis h adalah dua garis bersilangan. Garis g terletak pada bidang α dan garis h terletak pada bidang β. Jarak garis g ke garis h sama dengan panjang ruas garis yang tegak lurus dengan kedua bidang tersebut.

Baca Juga: Jarak Titik ke Garis
Cara Menetukan Jarak Garis ke Garis
Bagaimana cara menentukan jarak garis ke garis dapat dilihat pada cara menyelesaikan beberapa soal berikut.
Soal 1:
Diketahu kubus ABCD EFGH memiliki panjang rusuk 6 cm. Barapakah jarak garis AE ke garis CG?
Penyelesaian:
Kedudukan garis AE dan garis CG adalah sejajar yang terletak pada bidang ACGE.
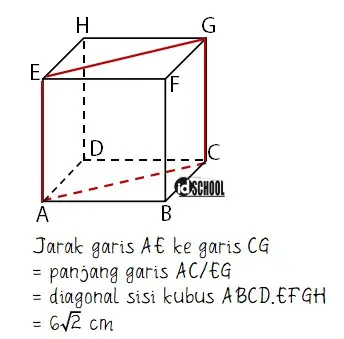
Jarak garis AE ke garis CG sama dengan diagonal sisi kubus ABCD EFGH. Sehingga jarak garis AE ke garis CG sama dengan rusuk√2 = 6√2 cm.
Soal 2:
Sebuah kubus ABCD.EFGH memiliki panjang rusuk 12 cm. Tentukan jarak garis BF ke garis EG!
Penyelesaian:
Langkah pertama untuk mendapatkan jarak garis BF ke garis EG adalah membuat bidang yang memuat garis EG dan sejajar dengan garis BF. Akan diperoleh bidang ACGE.
Selanjutnya, ambil satu titik pada garis BF dan proyeksikan pada bidang ACGE. Jarak setiap titik pada garis BF ke bidang ACGE sama dengan jarak garis BF ke garis EG.
Jarak garis BF ke garis EG sama dengan setengah diagonal sisi kubus ABCDE EFGH seperti yang ditunjukkan pada cara di bawah.

Baca Juga: Besar Sudut Antara Garis dan Bidang
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Jarak Garis ke Garis
Diketahui panjang rusuk kubus di atas adalah 10 cm. Titik P dan titik Q berturut-turut merupakan titik tengah dari rusuk AB dan BC.
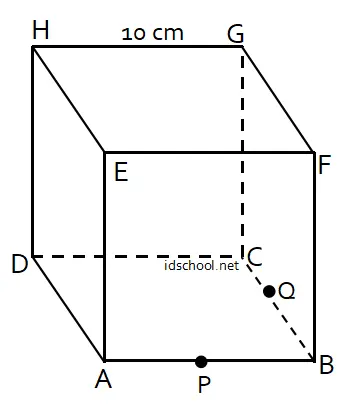
Jarak garis PQ ke garis EG adalah ….
A. 2/5√6 cm
B. 3/5√6 cm
C. 4/5√6 cm
D. 3/2√6 cm
E. 5/2√6 cm
Pembahasan:
Jarak garis PQ ke garis EG sama dengan panjang ruas garis yang tegak lurus dengan kedua garis tersbeut, yaitu garis MN pada gambar berikut.

Sebelum menghitung panjang MN perlu mencari panjang PQ, QN, BN, BR, dan NR terlebih dahulu. Panjang PQ, QN, BN, dan BR dapat dihitung dengan rumus Pythagoras. Sementara panjang NR sama dengan selilisih BR dan BN.
- PQ = 5√2 cm, sisi miring segitiga siku-siku sama kaki PBQ
- QN = 1/2PQ
QN = 1/2×5 = 5/2√2 cm
- 1/2×BN×PQ = 1/2×PB×BQ
BN × 5√2 = 5 × 5
BN = 25/5√2 = 5/2√2 cm
- NR = BR − BN
NR = 5√2 − 5/2√2 = 5/2√2 cm
Jarak garis PQ ke garis EG adalah panjang ruas garis MN. Cara menghitung panjang ruas garis MN dilakukan seperti langkah penyelesaian berikut.
Menghitung panjang MN:
MN2 = MR2 + RN2
MN2 = 102 + (5/2√2)2
MN2 = 100 + 50/4
MN2 = 100/4 + 50/4 = 150/4
MN = √150/4 = √(25×6)/√4
MN = 5√6/2 = 5/2√6 cm
Jadi panjang garis MN dengan garis EG adalah 5/2√6 cm.
Jawaban: E
Baca Juga: Pasangan Garis Saling Sejajar, Berpotongan, dan Bersilangan pada Kubus ABCD EFGH
Contoh 2 – Soal Jarak Garis ke Garis
Kubus ABCD EFGH memiliki panjang rusuk a cm. Jarak garis AE dan HB adalah ….
A. a√3 cm
B. a√2 cm
C. 1/2a√2 cm
B. 1/3a√3 cm
B. 1/2a√3 cm
Pembahasan:
Kedudukan garis AE dan HB pada kubus ABCD EFGH sesuai dengan gambar berikut.

Jarak garis AE dan garis HB sama dengan panjang ruas garis MN. Di mana proyeksi garis MN pada bidang ABCD adalah garis M’N’. Panjang ruang garis M’N’ sama dengan setengah diagonal sisi kubus ABCD EFGH.
Panjang diagonal sisi pada sebuah kubus adalah rusuk√2. Kubus ABCD EFGH memiliki panjang rusuk a cm, sehingga panjang diagonal sisinya adalah a√2 cm.
Jarak garis AE dan HB
= 1/2 × diagonal sisi kubus
= 1/2 × a√2 = 1/2a√2 cm
Jadi, jarak garis AE dan HB adalah 1/2a√2 cm.
Jawaban: C
Sekian pembahasan jarak garis ke garis pada kubus dalam dimensi tiga. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Hai Ras, pada langkah tersebut nilai 25 disamakan penyebutnya. Agar nilai 25 memiliki penyebut 4 maka harus dibuta menjadi 100/4 (nilai tersebut sama dengan 25, sehingga diperbolehkan)
G bisa.. harusnya kalo sama penyebut jadinya 50/4 + 400/4..
Halo Ahmad, penjelasan di atas merupakan langkah untuk mencari BN, kalau pada langkah mencari MN benar merubah 100 menjadi 400/4. Terimakasih sudah mengunjungi idschool, sukses selalu!