Jika ditentukan himpunan P = {x | x² − 3x ≤ 0} dan Q = {x | x² − 5x ≥ 0} maka P ∩ Q = ⋯
(A) 0
(B) {0}
(C) {0, 5}
(D) {3, 5}
(E) himpunan kosong

Jawab: (B)

• Dari soal diketahui:
  • P = {x | x² − 3x ≤ 0}
  • Q = {x | x² − 5x ≥ 0}

Anggota himpunan P himpunan adalah semua nilai x yang memenuhi pertidaksamaan kuadrat x² − 3x ≤ 0. Ada dua langkah untuk mendapatkan nilai x yang memenuhi pertidaksamaan. Dua langkah tersebut adalah mengambil harga nol dari pertidaksamaan kemudian menentukan daerah yang memenuhi.

Harga nol pertidaksamaan:

x² − 3x = 0

x(x − 3) = 0

x₁ = 0 atau x₂ = 3

Menentukan nilai x yang memenuhi pertidaksamaan x² − 3x ≤ 0 (anggota himpunan P):

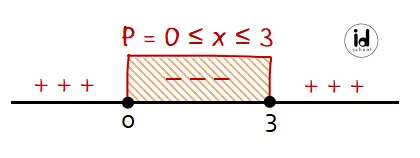
Anggota himpunan Q adalah semua nilai x yang memenuhi pertidaksamaan kuadrat x² − 5x ≥ 0. Untuk menentukan nilai x yang memenuhi pertidaksamaan dapat dilakukan melalui dua langkah penyelesaian seperti sebelumnya.

Harga nol pertidaksamaan:

x² − 5x = 0

x(x − 5) = 0

x₁ = 0 atau x₂ = 5

Menentukan nilai x yang memenuhi pertidaksamaan x² − 5x ≥ 0 (anggota himpunan Q):

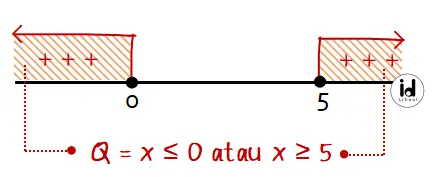
Operasi himpunan P ∩ Q menghasilkan anggota-anggota yang sama dari himpunan P dan Q. Diketahui anggota himpunan P = 0 ≤ x ≤ 3 dan anggota himpunan Q = x ≤ 0 atau x ≥ 5. Anggota himpunan P ∩ Q adalah anggota himpunan yang ada di himpunan P dan Q yaitu P ∩ Q = {0}, hanya ada satu anggota.

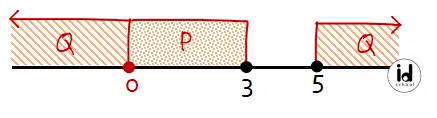
Sehingga, jika ditentukan himpunan P = {x | x² − 3x ≤ 0} dan Q = {x | x² – 5x ≥ 0} maka P ∩ Q = {0}.