Jumlah 24 suku pertama adalah ….

Dari barisan aritmetika diketahui U₃ = 18 dan U₇ = 38. Jumlah 24 suku pertama adalah ….
A. 786
B. 1.248
C. 1.572
D. 3.140

Jawab: C

Jumlah n suku pertama dapat dihitung dengan rumus Sn berikut.

Keterangan:
Sn = jumlah n suku pertama
a = suku pertama
b = beda/selisih suku ke-n dengan suku ke-(n ‒ 1)

Sehingga, untuk menghitung jumlah 24 suku pertama perlu diketahui nilai suku pertama (a) dan beda/selisih (b) terlebih dahulu.

Dari soal diketahui bahwa U₃ = 18 dan U₇ = 38. Rumus suku ke-n dari barisan aritmatika memenuhi persamaan Un = a + (n ‒ 1)b.

Sehingga, dari apa apa yang diketahui pada soal dapat dibentuk dua persamaan berikut.

• Persamaan (i):
  U₃ = 18
  a + 2b = 18

• Persamaan (ii):
  U₇ = 38
  a + 6b = 38

Nilai a dan b dapat dicari tahu dengan menyelesaikan sistem persamaan linear dua variabel dari persamaan (i) a + 2b = 18 dan (ii) a + 6b = 38. Cara mendapatkan nilai a dan b terdapat pada langkah penyelesaian berikut.

Mencari nilai b:
eliminasi a dari persamaan (i) dan (ii) untuk mendapatkan nilai b.

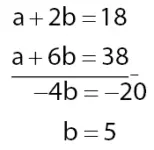
Diperoleh nilai b = 5, selanjutnya substitusi nilai b = 5 pada persaman (i) atau (ii) untuk mendapatkan nilai a.

Di sini akan digunakan persamaan a + 2b = 18.

Mencari nilai a:
a + 2b = 18
a + 2×5 = 18
a + 10 = 18
a = 18 ‒ 10 = 8

Menghitung jumlah 24 suku pertama:
S₂₄ = ²⁴/₂ × [2×8 + (24 ‒ 1)×5]
S₂₄ = 12 × (16 + 23×5)
S₂₄ = 12 × (16 + 115)
S₂₄ = 12 × 131 = 1.572

Jadi, jumlah 24 suku pertama adalah S₂₄ = 1.572