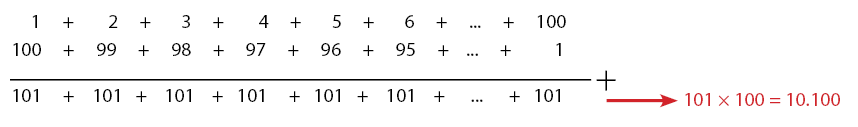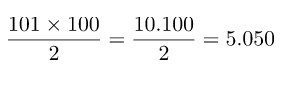Baris dan deret adalah bahasan materi yang mempelajari karakteristik dari pola baris/deret bilangan. Pola baris bilangan memiliki banyak bentuk antara lain pola bilangan asli, bilangan genap/ganjil, persegi, segitiga, dan alin sebagainya. Setiap pola barisan bilangan pada umumnya memiliki rumus umum yang berlaku pada setiap bilangan pada suatu baris atau deret. Misalnya pola bilangan 1, 2, 3, 4, …. memiliki rumus umum untuk setiap sukunya sama dengan n dengan n adalah bilangan asli.
Contoh lain, pola bilangan 1, 3, 5, 7, … adalah pola bilangan ganjil yang sesuai dengan rumus untuk setiap sukunya sama dengan 2n – 1, dengan n = bilangan asli. Untuk pola bilangan genap memiliki rumus untuk bilangan setiap sukunya sama dengan 2n dengan n = bilangan asli. Bentuk pola bilangan genap adalah 2, 4, 6, 8, …. Selain beberapa contoh yang telah disebutkan terdapat juga pola bilangan persegi dan segitiga. Pola biilangan persegi adalah 1, 4, 9, 16, … dengan rumus n2 (n bilangan asli). Sedangkan pola bilangan segitiga adalah 1, 3, 6, 10, … dengan rumus setiap sukunya adalah n/2×(n+1).
Baca Juga: Pola Barisan Dua Tingkat
Bagaimana bentuk rumus umum setiap suku pada suatu baris dan deret? Sobat idschool dapat mencari tahu lebih banyak lagi melalui pembahasan di bawah.
Table of Contents
- Materi Pengantar Baris dan Deret
- Baris dan Deret Aritmetika
- Baris dan Deret Geometri
- Contoh Soal dan Pembahasan
Materi Pengantar Baris dan Deret
Baris dan deret bilangan terdiri dari dua jenis yaitu aritmetika dan geometri. Rumus pada baris dan deret aritmetika ataugeometri berguna untuk memudahkan dalam menghitung sejumlah tertentu yang pastinya secara lebih cepat.
Contoh penggunaan rumus baris dan deret adalah menjumlahkan bilangan 1 sampai dengan 100. Coba hitung deret bilangan tersebut! Apakah jawaban yang kalian peroleh adalah 5050? Berapa waktu yang dibutuhkan untuk menghitungnya? Jika menghitung secara manual, pasti akan memakan waktu yang lama. Sekarang coba perhatikan trik berikut.
Perhatikan keunikan pada penjumlahan tiap kolom di atas. Seluruh kolom pada baris di atas, jumlah masing-masingnya adalah 101. Hasil di atas membentuk bilangan 101 sejumlah 100 kali. Dengan mudah, kita bisa mendapatkan hasilnya yaitu 101×100 = 10.100. Bilangan 101 sejumlah 100 kali terbentuk dari dua buah deret, sehingg untuk mengetahui jumlah satu deretnya maka hasil akhirnya perlu dibagi dua.
Begitulah cara cepat untuk mengetahui jumlah bilangan 1 sampai dengan 100. Hasil perhitungan tersebut dapat juga diperoleh menggunakan rumus baris dan deret.
Baris dan Deret Aritmetika
Barisan Aritmetika mempunyai ciri-ciri yaitu selisih/beda antara dua suku yang berurutan selalu sama atau tetap. Perhatikan dua contoh barisan Aritmetika di bawah yang meliputi barisan aritmerika naik dan barisan aritmetika turun.
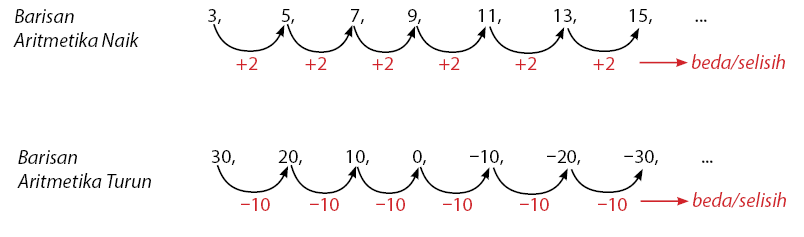
Suku ke-n menunjuk pada suku pada urutan ke-n, lebih jelasnya dapat dilihat pada gambar berikut.

Berdasarkan pola barisan aritmetika, terdapat rumus yang dapat digunakan untuk mempermudah mencari suku ke-n.
Un = a + (n ‒ 1)b
rumus suku ke-n pada barisan aritmatika
Keterangan:
Un = suku ke-n (n = 1, 2, 3. ….)
a = suku pertama
b = beda/selisih antara dua suku = Un ‒ Un‒1 = Un+1 ‒ Un
Penjumlahan suku-suku pada barisan aritmetika membentuk sebuah deret yang disebut dengan deret aritmetika.

Rumus di bawah dapat digunakan untuk mencari jumlah n suku pertama.
Sn = n/2×( a + Un)
atau
Sn = n/2×[2a + (n‒1)b]
Jumlah n suku pertama pada barisan aritmetika
Keterangan:
Sn = jumlah n suku pertama
Un = suku ke-n
a = suku pertama
b = beda/selisih antara dua suku = Un ‒ Un‒1 = Un+1 ‒ Un
Baca Juga: Cara Menentukan Satuan Bilangan Berpangkat Banyak
Baris dan Deret Geometri
Barisan Geometri mempunyai ciri-ciri memiliki perbandingan/rasio antara dua suku yang berurutan selalu sama atau tetap. Perhatikan dua contoh barisan Geometri di bawah yang meliputi barisan geometri naik dan barisan geometri turun.

Suku ke-n menunjuk pada suku pada urutan ke-n, lebih jelasnya dapat dilihat pada gambar berikut.
Berdasarkan pola barisan aritmetika, terdapat rumus yang dapat digunakan untuk mempermudah mencari suku-n.
Un = ar(n‒1)
Rumus suku ke-n pada Barisan Geometri
Keterangan:
Un = suku ke-n
a = suku pertama
r = rasio = Un/U(n‒1) = Un+1/Un
Penjumlahan suku-suku pada barisan geometri membentuk sebuah deret yang disebut dengan deret geometri.
Rumus di bawah dapat digunakan untuk mencari jumlah n suku pertama pada barisan dan deret geometri.
Baca Juga: Cara Menghitung Luas Selimut Kerucut
Contoh Soal dan Pembahasan
Beberapa contoh soal dibawah dapat sobat idschool gunakan untuk nambah pemahaman bahasan baris dan deret di atas. Setiap contoh soal baris dan deret yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Baris dan Deret
Seutas tali dipotong menjadi 5 bagian yang ukurannya membentuk deret geometri. Jika panjang potongan tali terpendek 4 cm dan panjang potongan tali terpanjang 324 cm, maka panjang tali semula adalah ….
A. 328 cm
B. 484 cm
C. 648 cm
D. 820 cm
Pembahasan:
Panjang tali membuat suatu barisan geometri U1, U2, U3, U4, dan U5 dengan tali terpendek: U1 = 4 cm dan tali terpanjang: U5 = 324 cm. Rasio dari deret geometri tersebut dapat diperoleh seperti cara berikut.
Mennetukan rasio dari deret geometri tersebut:
U5 = 324
ar4 = 324
4 × r4 = 324
r4 = 324/4
r4 = 81 → r = 3
Diperoleh barisan geometrinya menjadi:
U1 = a = 4 (diketahui)
U2 = ar2-1 = ar1 = 4 × 3 = 12
U3 = ar3-1 = ar2 = 4 × 9 = 36
U4 = ar4-1 = ar3 = 4 × 27 = 108
U5 = 324 (diketahui)
Jadi, panjang tali semula sama dengan 4 + 12 + 36 + 108 + 324 = 484 cm.
Jawaban: B
Contoh 2 – Soal Baris dan Deret
Suatu bakteri dapat membelah diri menjadi tiga setiap 13 menit. Jika banyak bakteri mula-mula berjumlah 20, diperlukan waktu t agar jumlah bakteri menjadi 14.580. Jika bakteri tersebut membelah diri menjadi tiga setiap 26 menit, banyaknya bakteri setelah waktu t adalah ….
A. 108 bakteri
B. 216 bakteri
C. 432 bakteri
D. 540 bakteri
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Banyak bakteri mula-mula: U1 = a = 20
- Kemampuan membelah diri menjadi 3 setiap 13 menit: r1 = 3 (setiap 13 menit)
- Banteri setelah waktu t (untuk rasio pertama): Un = 14.580
- Kemampuan membelah diri menjadi 3 setiap 13 menit: r2 = 3 (setiap 26 menit)
Menghitung banyaknya n kali pembelahan yang terjadi untuk pembelahan yang terjadi dengan r1 = 3 setiap 13 menit:
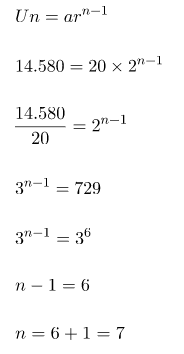
Pembelahan terjadi sebanyak = 7 – 1 = 6 kali pembelahan. Sehingga, lama waktu pembelahan yang terjadi adalah selama 6 × 13 = 91 menit.
Selanjutnya gunakan r2 = 3 di mana waktu pembelahan terjadi selama 26 menit. Banyaknya n pembelahan yang akan terjadi adalah sebanyak = 78 : 26 = 3 (mencari suku ke – 4).
Mencari banyaknya bakteri setelah terjadi 3 kali pembelahan (U4):
Un = a × rn – 1
U4 = 20 × 34 – 1
U4 = 20 × 33
U4 = 20 × 27
U4 = 540
Jadi, jika bakteri tersebut membelah diri menjadi tiga setiap 26 menit banyaknya bakteri setelah waktu t adalah 540 bakteri.
Jawaban: D
Sekian ulasan materi baris dan deret yang dilengkapi dengan contoh soal dan pembahasan. Terimakasih sudah mengunjungi idschool.net, semoga bermanfaat!
Baca Juga: Cara Menentukan Rumus Un dari Suatu Pola Bilangan