Sebuah suku ke-5 sebuah deret aritmetika adalah 11 dan jumlah nilai suku ke-8 dengan suku ke-12 sama dengan 52. Jumlah 8 suku pertama deret tersebut adalah ….
A. 68
B. 72
C. 76
D. 80
E. 84
Jawab: C
Berdasarkan keterangan yang diberikan pada soal dapat diketahui nilai suku ke 5 (U5) serta jumlah suku ke 8 (U8) dengan suku ke 12 (U12) dari suatu deret aritmatika.
Rumus suku ke n dari deret aritmatika:
Un = a + (n − 1)b
Sehingga dapat dibentuk dua persamaan linear dua variabel (SPLDV) seperti berikut.
- U5 = 11
a + 4b = 11
- U8 + U12 = 52
(a + 7b) + (a + 11b) = 52
2a + 18b = 52
a + 9b = 26
Nilai suku pertama (a) dan beda (b) dari deret aritmatika tersebut dapat diperoleh dengan menyelesaikan sistem persamaan linear (i) a + 4b = 11 dan (ii) a + 9b = 26 dengan metode eliminsai/substitusi.
Menentukan nilai b:
Eliminasi a dari persamaan (i) dan (ii) untuk mendapatkan nilai b seperti penyelesaian berikut.
Menentukan nilai a:
Substitusi hasil perhitungan b = 3 pada persamaan (i) a + 4b = 11 untuk mendapatkan nilai a.
a + 4b = 11
a + 4×3 = 11
a + 12 = 11
a = 11 − 12 = −1
Diperoleh hasil perhitungan nilai suku pertama deret arimatika tersebut adalah a = −1 dan beda b = 3. Kedua nilai tersebut digunakan untuk menghitung jumlahl 8 suku pertama deret aritmatika tersebut.
Rumus jumlah n suku pertama deret aritmatika:
Cara menghitung jumlah 8 suku pertama deret tersebut adalah,
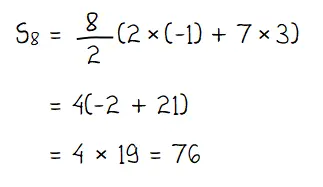
Jadi, jumlah 8 suku pertama deret tersebut adalah S8 = 76