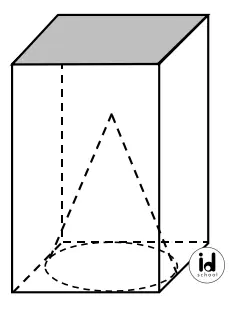
Kerucut dengan tinggi 15 terletak di dalam balok. Alas kerucut sebidang dengan alas balok dan menyinggung keempat sisinya. Alas balok berbentuk persegi dengan sisi 20. Volume bagian balok di luar kerucut 7 kali volume kerucut. Luas permukaan balok adalah ….

(B) 800 + 400π

(C) 800 + 800π

(D) 800 + 1.200π

(E) 800 + 2.400π

Jawab: (C)

Dari soal dapat diketahui:

• Kerucut dengan tinggi 15 terletak di dalam balok.
• Alas kerucut sebidang dengan alas balok dan menyinggung keempat sisinya
• Alas balok berbentuk persegi dengan sisi 20.
• Volume bagian balok di luar kerucut 7 kali volume kerucut.

Dari informasi tersebut dapat diperoleh ukuran-ukuran kerucut dengan tinggi 15 terletak di dalam balok dan balok tersebut pada gambar di bawah.

Untuk menghitung luas permukaan balok dilakukan melalui beberapa perhitungan berikut.

1) Menghitung volume kerucut:

V kerucut = ¹/₃ × π × r² × t

V = ¹/₃ × π × 10² × 15 = 500π

2) Menghitung volume balok:

V balok = V balok di luar kerucut + V kerucut

V balok = 7 × volume kerucut + V kerucut

V balok = 8 × volume kerucut

V balok = 8 × 500π = 4.000π

3) Menghitung tinggi balok:

V balok = 4.000π

p × l × t = 4.000π

20 × 20 × t = 4.000π

400t = 4.000π

t = ^4.000π/₄₀₀ = 10π

4) Menghitung luas permukaan balok:

Luas balok = 2(p×l + p×t + l×t)

Luas balok = 2(20×20 + 20×10π + 20×10π)

Luas balok = 2(400 + 400π) = 800 + 800π

Jadi, luas permukaan balok tersebut adalah (C) 800 + 800π.