UTBK 2024
Koordinat titik-titik sudut segitiga ABC adalah A(1, 1), B(1, 3), dan C(d, 2). Apakah garis y = mx memotong segitiga ABC?
Putuskan apakah pernyataan (1) dan (2) berikut cukup untuk menjawab pertanyaan tersebut.
(1) m > 1 dan d < 1
(2) m > 0 dan d < 0
(A) Pernyataan (1) SAJA cukup untuk mejawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
(B) Pernyataan (2) SAJA cukup untuk mejawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
(C) DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi satu pernyataan SAJA tidak cukup.
(D) Pernyataan (1) SAJA cukup untuk mejawab pertanyaan dan pernyataan (2) SAJA cukup.
(E) Pernyataan (1) dan pernyataan (2) tidak cukup untuk mejawab pertanyaan.
Jawab: (C)
Untuk pernyataan (1): m > 1 dan d < 1
Saat m > 1, garis y = mx memiliki gradien positif sehingga garis lurus condong ke kanan. Untuk nilai m > 1 maka garis pasti akan memotong ruas sisi AB karena sisi AB memiliki koordinat titik paling bawah A(1, 1). Dengan otomatis akan memotong segitiga ABC.
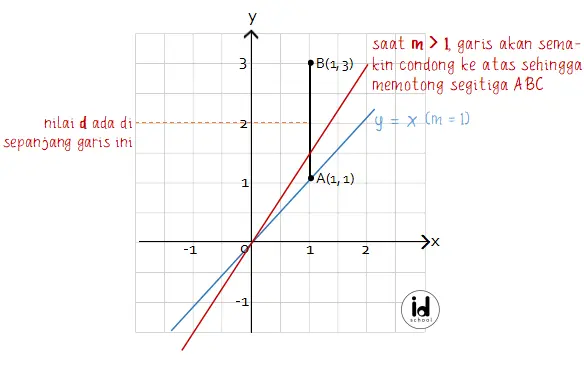
Namun kondisi ini hanya terjadi saat nilai m < 3. Saat nilai m > 3 dan d < 1 untuk nilai d sangat mendekati bilangan 1, garis y mx dapat tidak memotong garis AB sehingga tidak memotong segitigai ABC. Minimal titik koordinat C yang dapat dipotong oleh garis y = mx untuk x = 3 adalah (2/3, 2).
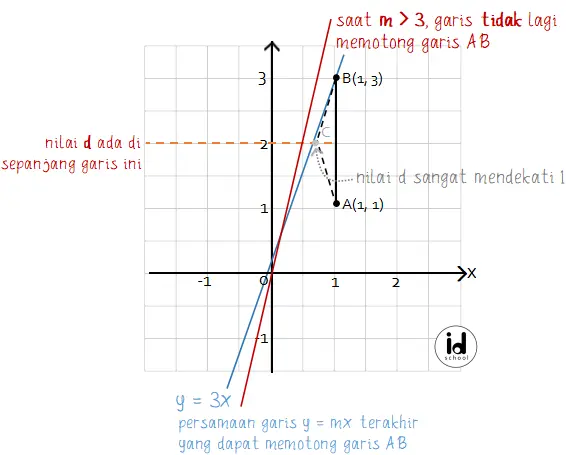
Ada dua kemungkinan yang terjadi saat nilai m > 0 dan d < 1 yaitu garis y = mx memotong segitiga ABC dan garis y = mx tidak memotong segitiga ABC. Jadi, pernyataan (1) tidak dapat digunakan untuk menjawab pertanyaan.
Untuk pernyataan (2): m > 0 dan d < 0
Saat m > 0, garis y = mx memiliki gradien positif sehingga garis lurus condong ke kanan. Untuk nilai m > 0, ada saat garis y = mx tidak menyinggung garis AB dan ada saat garis y = mx menyinggung garis AB. Garis y = mx hanya akan memotong segitiga ABC saat m > 1.
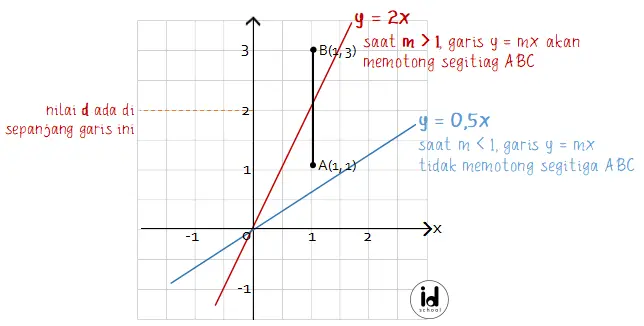
Untuk m > 0, garis y = mx dapat memotong segitiga ABC dan garis y = mx dapat juga tidak memotong segitiga ABC. Ada dua kemungkinan sehingga tidak dapat digunakan untuk menjawab pertanyaan.
Jadi, pernyataan (2) tidak dapat digunakan untuk menjawab pertanyaan.
Untuk pernyataan (1) m > 1 dan d < 1 + (2) m > 0 dan d < 0:
Gabungan kedua syarat pada pernyataan (1) dan (2) menghasilkan syarat nilai m > 1 dan d < 0.
Untuk m > 1, garis y = mx pasti akan memotong garis AB saat nilai m ≤ 3. Sehingga garis y = mx akan selalu memotong segitiga ABC saat nilai 3 ≥ m > 1.
Selanjutnya untuk nilai m > 3, nilai maksimal m = tak hingga berupa garis y = mx merupakan garis vertikal pada sumbu y yang pasti memotong titik koordinat C saat d = 0 yaitu C(0, 2).
Garis y = mx akan memotong garis AB saat selang nilai 1 < m ≤ 3 dan d < 0 dan garis y = mx akan memotong garis AC dan BC saat nilai m > 3 dan d < 0. Jadi, dapat dipastikan bahwa garis y = mx memotong segitiga ABC saat terdapat informasi (1) m > 1 dan d < 1 serta (2) m > 0 dan d < 0.
Kesimpulan: DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi satu pernyataan SAJA tidak cukup.