limx→2 (
2x2 − 8x − 2 +
x2 − 2x2x − 4) = ….
A. 5
B. 6
C. 8
D. 9
E. ~
Jawab: D
Soal di atas dapat lebih cepat dan muda dikerjakan dengan Aturan L’ Hospital karena hasil substitusi nilai x yang mendekati fungsi menghasilkan bentuk tak tentu 0/0 seperti perhitungan berikut.
limx→2 (
2x2 − 8x − 2 +
x2 − 2x2x − 4)
=
2(22) − 82 − 2 +
22 − 2(2)2(2) − 4 =
0 0 Cara Menentukan nilai limit limx→2 (2x2 − 8/x − 2 + x2 − 2x/2x − 4) dengan Aturan L’ Hospital:
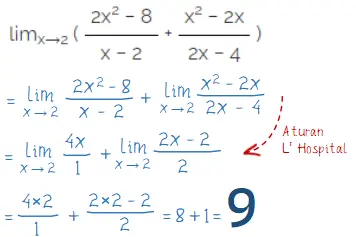
Selain dengan Aturan L’ Hospital, nilai limit dari lim x – 2 {(2x^2 – 8)/(x – 2) + (x^2 – 2x)/(2x – 4)} = dapat juga ditentukan dengan metode pemfaktoran. Cara menentukan nilai limit dari soal dengan metode pemfaktoran aljabar terdapat pada langkah penyelesaian berikut.

Jadi, nilai lim x – 2 {(2x^2 – 8)/(x – 2) + (x^2 – 2x)/(2x – 4)} = 9.