Jika ditentukan himpunan P = {x| x² − x − 6 ≤ 0}, dan H = {x| x² − x − 2 > 0} maka himpunan P – H adalah ….
(A) {−2 ≤ x < −1} 
(B) {−1 ≤ x ≤ 2}
(C) {2 < x ≤ 3 }  
(D) {−1 < x ≤ 3}  
(E) {−1 ≤ x < 2} 

Jawab: (B)

• Dari soal diketahui:
  • P = {x | x² − x − 6 ≤ 0}
  • H = {x | x² − x − 2 > 0}

Anggota himpunan P adalah semua nilai x yang memenuhi pertidaksamaan x² − x − 6 ≤ 0. Nilai x yang memenuhi pertidaksamaan tersebut diperoleh dengan cara mengambil harga nol dan melakukan pemfaktoran persamaan kuadrat seperti berikut.

Harga nol:

x² − x − 6 = 0 

(x − 3)(x + 2) = 0

x₁ = 3 atau x₂ = −2

Menentukan nilai x yang memenuhi pertidaksamaan kuadrat x² − x − 6 ≤ 0:

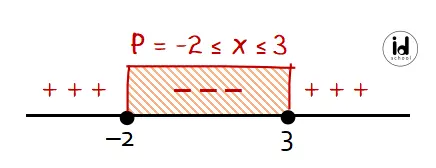
Sehingga dapat diketahui bahwa anggota himpunan P = {−2 ≤ x ≤ 3}.

Anggota himpunan H adalah semua nilai x yang memenuhi pertidaksamaan x² − x − 2 > 0. Nilai x yang memenuhi pertidaksamaan tersebut diperoleh dengan cara mengambil harga nol dan melakukan pemfaktoran persamaan kuadrat seperti berikut.

Harga nol:

x² − x − 2 = 0 

(x + 1)(x − 2) = 0

x₁ = −1 atau x₂ = 2

Menentukan nilai x yang memenuhi pertidaksamaan x² − x − 2 > 0:

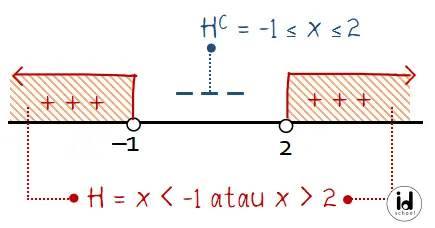
Sehingga dapat diketahui bahwa anggota himpunan H = {x < −1 atau x > 2} dan H^C = {−1 ≤ x ≤ 2}.  

Diperoleh anggota himpunan P = {−2 ≤ x ≤ 3} dan H^C = {−1 ≤ x ≤ 2}. Anggota himpunan P − H sama dengan anggota himpunan P ∩ H^C.

Sehingga,

P − H =  P ∩ H^C

= {−2 ≤ x ≤ 3} ∩ {−1 ≤ x ≤ 2}

= {−1 ≤ x ≤ 2}

Jadi, himpunan P − H adalah −1 ≤ x ≤ 2 (B)