UTBK 2024
Jika 1 < c < 3, maka semua nilai x yang memenuhi pertidaksamaan
adalah ….
(A) x < –1 atau x > 2
(B) x < –2 atau x > 3
(C) –2 < x < 2
(D) –3 < x < 2
(E) –2 < x < 3
Jawab: (E)
1) Menentukan pembuat nol pembilang:
(3 – x)(x + 2) = 0
3 – x = 0 atau x + 2 = 0
x = 3 atau x = –2
2) Menentukan pembuat nol penyebut:
Periksa nilai diskriman (D) dari persamaan penyebut.
D = 32 – 4×(–1)×(–3c)
D = 9 – 12c
Diketahui nilai c berada pada selang 1 < c < 3, sehingga nilai diskriminan D akan selalu negatif (D < 0). Untuk nilai D < 0 pada suatu persamaan kuadrat tidak memiliki pembuat nol.
3) Menentukan himpunan penyelesaian:
Garis bilangan yang akan digunakan:

Lakukan titik uji, ambil nilai x = 0 dan substitusi ke persamaan pembilang dan penyebut. Hasilnya adalah penyebut bernilai positif dan pembilang bernilai negatif. Nilai untuk pertidaksamaan menjadi positif dibagi negatif, hasilnya adalah negatif.
Kesimpulannya adalah daerah yang memuat angka nol (0) bernilai negatif. Untuk daerah kanan kirinya akan menjadi positif seperti berikut.
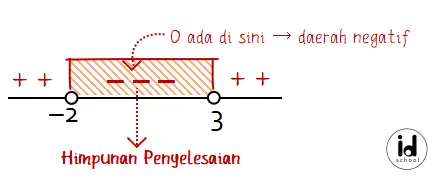
Pertidaksamaan pecahan yang diberikan berupa kurang dari sehingga himpunan penyelesaian yang memenuhi adalah daerah negatif. Maka semua nilai x yang memenuhi pertidaksamaan tersebut adalah x = {–2 < x < 3} (E).