Nilai x yang memenuhi pertidaksamaan di atas adalah ….

Diketahui,

Nilai x yang memenuhi pertidaksamaan di atas adalah ….
A. {x | ‒⁷/₆<x<2 atau x > 3, x∊R}
B. {x | x<‒3 atau ‒⁷/₆<x< 2, x∊R}
C. {x | ‒3<x<1 atau x>2, x∊R}
D. {x | ‒3<x<1 atau x>⁷/₆, x∊R}
E. {x | x<‒3 atau ⁷/₆<x<2, x∊R}

Jawab: E

Untuk mendapatkan nilai x yang memenuhi pertidaksamaan kuadrat perlu dilakukan operasi aljabar untuk mendapatkan bentuk paling sederhana terlebih dahulu.

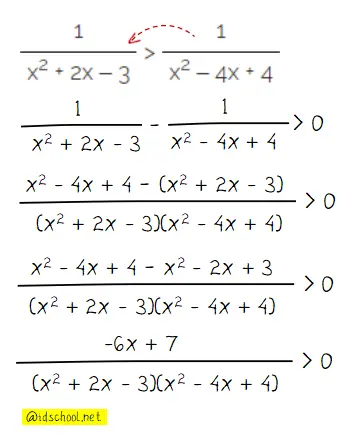
Harga nol untuk pembilang:

• ‒6x+7 = 0
  ‒6x = ‒7
  x = ⁷/₆

Harga nol untuk penyebut:

• x²+2x‒3 = 0
  (x+3)(x‒1) = 0
  x = ‒3 atau x = 1

• x²‒4x+4 = 0
  (x‒2)(x‒2) = 0
  x = 2

Diperoleh batas interval: x₁ = ‒3; x₂ = 1; x₂ = ⁷/₆; dan x₄ = 2. Ada 5 daerah interval yang perlu diuji nilai positif/negatifnya. Ambil titik uji untuk setiap daerah dan cari tahu nilai yang dihasilkan seperti yang dilakukan pada cara berikut.

• Daerah satu (ambil nilai x < ‒3): x = ‒4
  ^‒6(‒4)+7/_{(16+2(‒4)‒3)(16‒4(‒4)+4)}
  = ^{24 + 7}/_{(16‒8‒3)(16+16+4)}
  = ³¹/_(5)(36) > 0 → positif

• Daerah dua (ambil nilai ‒3 < x < 1): x = 0
  ^‒6(0)+7/_{(0+2(0)‒3)(1‒4(‒1)+4)}
  = ⁰⁺⁷/_(‒3)(6)
  = ⁷/_(‒3) < 0 → negatif

• Daerah tiga (ambil nilai 1 < x < ⁷/₆): x = 1,1
  ^{‒6(1,1) + 7}/_{(1,21+2(1,1)‒3)(1,21‒4(1,1)+4)}
  = ^‒6,6+7/_{(1,21+2,2‒3)(1,21‒4,4+4)}
  = ^0,4/_(0,41)(0,81) > 0 → positif

• Daerah empat (ambil nilai ⁷/₆ < x < 2): x = 1,5
  ^‒6(1,5)+7/_{(2,25+2(1,5)‒3)(2,25‒4(1,5)+4)}
  = ^‒9+7/_{(2,25+3‒3)(2,25‒6+4)}
  = ^‒2/_(2,25)(0,25) < 0 → negatif

• Daerah lima (ambil nilai x > 2): x = 3
  ^‒6(3)+7/_{(9+2(3)‒3)(9‒4(3)+4)}
  = ^‒18+7/_{(9+6‒3)(9‒12+4)}
  = ^‒11/_(12)(1) <0 → negatif

Dengan perhitungan menggunakan titik uji dapat diperoleh nilai-nilai yang menghasilkan himpunan penyelesiaan x yang memenuhi pertidaksamaan seperti garis bilangan berikut.

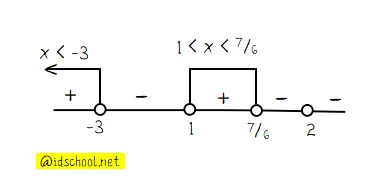
Nilai x yang memenuhi pertidaksamaan di atas adalah daerah yang menghasilkan nilai positif. Jadi, nilai x yang memenuhi pertidaksamaan di atas adalah {x | x < ‒3 atau ⁷/₆ < x < 2, x ∊ R}