Nilai x yang memenuhi (x+1)(x+2) ≥ (x+2) adalah ….
(A) x ≤ −1 atau x ≥ 1
(B) x ≤ −2 atau x ≥ 2
(C) x ≤ −2 atau x ≥ 0
(D) −1 ≤ x ≤ 1
(E) −2 ≤ x ≤ 0
Jawab: (C)
Menyederhanakan bentuk pertidaksamaan:
(x+1)(x+2) ≥ (x+2)
x2 + 3x + 2 ≥ x + 2
x2 + 3x − x + 2 − 2 ≥ 0
x2 + 2x ≥ 0
x(x + 2) ≥ 0
Diperoleh bentuk pertidaksamaan kuadrat. Cara menentukan himpunan penyelesaian pertidaksamaan kuadrat dengan mencari semua bilangan real yang memenuhi pertidaksamaan.
Pertama, tentukan nilai-nilai yang menghasilkan nol. Caranya dengan mengambil harga nol dari bentuk pertidaksamaannya seperti yang dilakukan pada cara berikut.
Harga nol:
x(x + 2) = 0
x1 = 0 atau x2 = –2
Diperoleh dua nilai x yaitu x1 = 0 dan x2 = –2 sehingga garis bilangan akan terbagi menjadi tiga yaitu di kiri -2, antara -2 sampai 0, dan di kanan 0. Selanjutnya lakukan uji titik untuk mengetahui daerah mana yang bernilai positif dan daerah mana yang bernilai negatif.
Caranya, ambil satu titik (sembarang, biasanya akan dipilih titik yang paling mudah untuk dihitung) di salah satu daerah kemudian substitusikan ke persamaan. Jika hasil substitusi menghasilkan nilai positif, maka daerah tersebut menghasilkan nilai positif. Sebaliknya jika hasil substitusi adalah negatif, maka daerah tersebut menghasilkan nilai negatif.
Contoh, ambil titik x = 1 yang terletak di kanan x = 0 kemudian susbtitusi nilai tersebut pada persamaan f(x) = x(x + 2).
Substitusi x = 1:
x(x + 2) = 1(1 + 2)
= 1 × 3
= 3
Diperoleh hasil positif, sehingga daerah di kanan nilai x = 0 adalah positif.
Daerah di sampingnya akan berkebalikan karena persamaan kuadrat memiliki akar tunggal. Sehingga dapat diperoleh daerah positif/negatif untuk ketiga daerah seperti berikut.
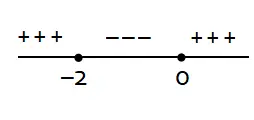
Himpunan penyelesaian untuk bentuk pertidaksamaan x(x + 2) ≥ 0 adalah daerah positif karena pertidaksamaan menyatakan lebih dari sama dengan nol. Sehingga himpunan penyelesaiannya adalah daerah yang berada di kiri x = -2 atau di kanan x = 0 seperti berikut.
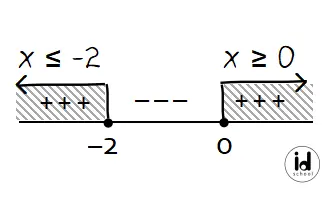
Jadi, nilai x yang memenuhi (x+1)(x+2) ≥ (x+2) adalah (C) x ≤ −2 atau x ≥ 0.