Contoh soal regresi linear sederhana dapat dikerjakan melalui dua cara yaitu perhitungan manual (tanpa software) dan perhitungan dengan software. Pengerjaan secara manual dapat memberikan pemahaman yang lebih akan asal nilai-nilai dalam analisis regresi sederhana diperoleh. Di mana pengerjaan contoh soal regresi linear sederhana secara manual dilakukan dengan melakukan perhitungan menggunakan rumus-rumus regresi linear sederhana.
Sayangnya pengerjaan contoh soal regresi linear sederhana secara manual akan sangat rumit untuk data yang sangat banyak. Sehingga pengerjaan contoh soal regresi linear sederhana untuk data yang sangat banyak lebih baik dilakukan dengan alat bantu atau software. Beberapa software yang dapat digunakan antara lain excel, Minitab, SPSS, R, Eviews, SAS, dan lain sebagainya. Secara umum penggunaan beberapa software akan mempermudah pekerjaan dalam melakukan analisis regresi linear sederhana.

Baca Juga: Perbedaan Statistik Deskriptif dan Inferensial
Untuk contoh soal regresi linear sederhana dengan kecil/sedikit dapat dilakukan tanpa software atau secara manual. Bagaimana cara penyelesaian contoh soal regresi linear sederhana secara manual? Apa saja rumus yang dibutuhkan dalam pengerjaan contoh soal regresi linear sederhana? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Contoh Soal Regresi Linear Sederhana
- Cara Menghitung dan Menentukan Persamaan Regresi Linear Sederhana
- Interpretasi model
- Hubungan (Korelasi) Variabel Besar Iklan dan Pendapatan
- Menyelidiki Signifikansi dan Pengujian Hipotesis
- Melakukan Prediksi
Contoh Soal Regresi Linear Sederhana
Cara menyelesaikan contoh soal regresi linear sederhana akan ditunjukkan melalui penyelesaian sebuah masalah sederhana. Persoalan menyangkut bagaimana membentuk model dan aplikasi model untuk melakukan prediksi. Selain itu juga akan ditunjukkan bagaimana interpretasi setiap hasil perhitungan yang dilakukan pada penyelesaian contoh soal regresi linear sederhana.
Soal:
Sebuah perusahaan ingin mengetahui bagaimana pengaruh besarnya iklan terhadap jumlah pendapatan yang diterima. Perusahaan tersebut memiliki data biaya iklan dan pendapatan seperti yang ditunjukkan tabel berikut (dalam satuan juta rupiah).
| Biaya Iklan | Pendapatan |
| 15 | 65 |
| 13 | 61 |
| 14 | 60 |
| 15 | 63 |
| 13 | 59 |
| 14 | 62 |
| 12 | 56 |
| 14 | 62 |
| 13 | 60 |
| 12 | 61 |
Tentukanlah:
i) Persamaan regresi linear sederhana
ii) Biaya iklan yang dikeluarkan untuk memperoleh pendapatan Rp35.000.000,00
Secara umum, langkah pengerjaan contoh soal regresi linear sederhana meliputi beberapa tahapan berikut.
- Mencari tahu apakah variabel-variabel memiliki hubungan linear atau tidak. Caranya dapat dilakukan dengan mengamati diagram pencar dari variabel-variabel yang digunakan.
- Menentukan mana variabel terikat (X) dan mana variabel bebas (Y).
- Menghitung nilai koefisien regresi (β0 dan β1)
- Mendapatkan model yang sesuai dengan data pada soal regresi linear sederhana
Baca Juga: Cara Membaca Boxplot (Diagram Kotak Garis)
Cara Menghitung dan Menentukan Persamaan Regresi Linear Sederhana
Bentuk diagram pencar yang sesuai untuk model regresi linear memiliki kecenderungan membentuk suatu garis lurus. Untuk data seperti yang diberikan pada contoh soal regresi linear sederhana memiliki diagram pencar seperti berikut.
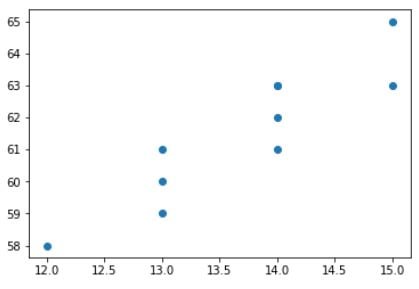
Melalui pengamatan dapat diketahui bahwa bentuk plot data membentuk suatu garis lurus sehingga dapat menggunakan model regresi linear. Di manan tujuan umum analisis regresi linear sederhana adalah untuk mengetahui pengaruh variabel bebas terhadap variabel terikat.
Rumus regresi linear sederhana memenuhi bentuk persamaan umum: Y = β0 + β1X. Di mana Y adalah variabel terikat (dependent variable), X adalah variabel bebas (independent variable), serta β0 dan β1 adalah koefisien regresi.
Rumus yang digunakan untuk menentukan nilai β0 dan β1 sesuai dengan persamaan-persamaan berikut.
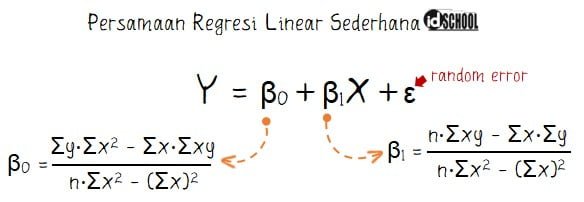
Dari data yang diberikan dapat diketahui bahwa varibel bebas adalah biaya iklan (x) dan variabel terikat adalah pendapatan (y). Dalam perhitungan koefisien regresi β0 dan β1 dibutuhkan nilai Σx, Σy, Σxy, Σx2, dan Σx2. Untuk mempermudah perhitungan perlu dibuat tabel perhitungan seperti yang ditunjukkan berikut.

Beberapa nilai dari isi tabel di atas dapat membantu perhitungan koefisien regresi β0 dan β1. Cara menghitung kedua koefisien regresi untuk membentuk model persamaan regresi linear sederhana dilakukan seperti cara penyelesaian berikut.
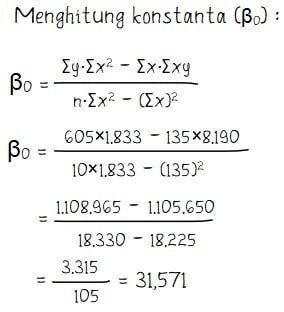

Dari perhitungan diperoleh nilai β0 = 31,571 dan β1 = 2,143 sehingga diperoleh model persamaan regresi linear sederhana sesuai data perusahaan tersebut adalah Y = 31,571 + 2,143X.
Baca Juga: Cara Membuat Tabel Distribusi Frekuensi Berdasarkan Aturan Sturgess
Interpretasi model
Dari hasil perhitungan diperoleh koefisien regresi β0 dan β1 sehingga didapat model persamaan regresi Y = 31,571 + 2,143X. Makna dari persamaan regresi dapat dipahami seperti interpretasi berikut.
- Nilai β0 = 31,571 artinya saat tidak mengunakan iklan atau biaya untuk iklan sama dengan nol (iklan = 0) maka pendapatan yang diperoleh adalah 31,571 juta rupiah.
- Nilai koefisien regresi β1 = 2,143 memberikan keterangan bahwa untuk setiap kenaikan satu satuan iklan (satu juta rupiah) maka meningkatkan pendapatan sebesar 2,143 juta rupiah.
Hubungan (Korelasi) Variabel Besar Iklan dan Pendapatan
Kuatnya hubungan antar variabel dapat diukur melalui nilai koefisien korelasi (r) yang nilainya berada pada rentang ‒1 sampai 1. Sementara kuadrat dari korelasi disebut dengan koefisien determinasi (KD atau R2) yang nilainya menunjukkan seberapa besar pengaruh variabel bebas terhadap variabel terikat.
Nilai korelasi pada analisis regresi linear sederhana dapat dihitung melalui rumus berikut.

Diperoleh nilai korelasi untuk data iklan dan pendapatan yang diperoleh adalah r = 0,908. Besar nilai tersebut menunjukkan hubungan positif yang sangat kuat antara biaya iklan yang dikeluarkan dengan pendapatan yang diperoleh.
Untuk besar nilai koefisien determinasi dapat diperoleh dari kuadrat nilai korelasi. Sehingga besar nilai koefisien determinasi sama dengan KD = R2 = 0,9082 = 0,824.
Dari nilai koefisien determinasi R2 = 0,824 dapat dimaknai bahwa variabel biaya iklan mampu menjelaskan besar pendapat yang diterima sebesar 82,4%. Sementara sisanya 18,6% dijelaskan oleh peubah atau variabel lain di luar persamaan.
Baca Juga: Contoh Cara Mengerjakan Statistik Deskriptif dengan Google Spreadsheet
Menyelidiki Signifikansi dan Pengujian Hipotesis
Pengujian hipotesis bahwa x tidak memberikan kontribusi untuk prediksi y dapat dilakukan melalui uji linearitas. Salah satu cara yang dapat dilakukan untuk menguji hubungan linear antara dua variabel dapat menggunakan koefisien korelasi.
Caranya dilakukan dengan membandingkan besar nilai t tabel dan t hitung. Untuk nilai t tabel dapat diperoleh dari tabel uji t. Sementara nilai t hiung dapat dipeorleh melalui perhitungan menggunakan rumus berikut.
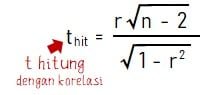
Di mana cara menentukan keputusan daerah penolakan H0 (daerah kritis) dilakukan dengan membandingkan t hitung dengan t tabel. Jika nilai hasil perhitungan t hitung lebih kecil dari t tabel maka H0 diterima atau H1 ditolak. Jika nilai hasil perhitungan t hitung lebih besar dari t tabel maka H0 ditolak atau H1 diterima.
Apakah terdapat hubungan yang signifkan antara biaya iklan yang dikeluarkan dengan pendapatan yang diperoleh dilakukan melalui pengujian hipotesis berikut.
Hipotesis:
H0 : β0 = 0 (tidak terdapat hubungan yang signifkan)
H1 : β0 ≠ 0 (terdapat hubungan yang signifikan)
Tingkat signifikansi: α = 5%
Statistik uji: tolak H0 jika |thitung| > t(0.025, 8)

Keputusan:
Tolak H0 karena |thitung| = 6,121 > 2,306 (ttabel), sehingga dapat disimpulkan bahwa terdapat hubungan yang signifikan antara pengeluaran biaya iklan dengan pendapatan yang diterima.
Melakukan Prediksi
Nilai perkiraan pendapatan yang diperoleh saat mengeluarkan biaya iklan sebesar Rp35.000.000,00 dihitung melalui subsitutsi X = 35 ke pesamaan Y. Di atas didapat persamaan regresi Y = 31,571 + 2,143X. Sehingga prediksi besar pendapatan yang akan diterima untuk biaya iklan sebesar X = 35 dihitung seperti cara berikut.
Melakukan prediksi:
Y = 31,571 + 2,143X
Y = 31,571 + 2,143(35)
Y = 31,571 + 75,005
Y = 106,576
Sehingga dapat diketahui prediksi pendapatan yang diperoleh dengan pengeluaran biaya iklan sebesar 35 juta rupiah adalah 106,576 juta rupiah.
Demikianlah tadi ulasan bagaimana cara menyelesaikan contoh soal regresi linear sederhana beserta interpretasinya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: 2 Macam Analisis Regresi Linear