Sebuah matriks A,

Persamaan garis 3x ‒ y ‒ 11 = 0 karena refleksi terhadap garis y = x, dilanjutkan oleh transformasi yang bersesuaian dengan matriks A adalah ….
A. ‒2x ‒ 7y ‒11 = 0
B. 2x + 7y ‒ 11 = 0
C. ‒2x ‒ 7y + 11 = 0
D. 2y ‒ 7x + 11 = 0
E. 2x ‒ 7y + 11 = 0
Jawab: E
Hasil pencerminan titik P(x, y) terhadap garis y = x adalah P'(y’, x’), sehingga diperoleh bersamaan x = y’ dan y = x’.
Substitusi kedua persamaan tersebut pada persamaan garis 3x ‒ y ‒ 11 = 0 untuk mendapatakan hasil persamaan garis 3x ‒ y ‒ 11 = 0 karena refleksi terhadap garis y = x seperti yang dilakukan pada cara berikut.
3x ‒ y ‒ 11 = 0
3y’ ‒ x’ ‒ 11 = 0
‒x’ + 3y’ ‒ 11 = 0
Misalkan hasil transformasi setiap titik pada garis ‒x’ + 3y’ ‒ 11 = 0 dengan matriks A adalah x” dan y”. Hasil transformasi garis oleh matriks A memenuhi persamaan berikut.
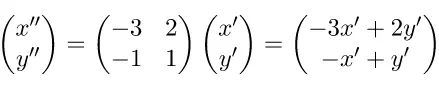
Operasi hitung matriks di atas menghasilkan dua persamaan yaitu (i) ‒3x’ + 2y’ = x’’ dan (ii) ‒x’ + y’ = y’’.
Selanjutnya perlu dicari persamaan x’ dan y’ yang memenuhi persamaan (i) dan (ii). Cara mencari nilai x’ dan y’ dilakukan seperti langkah penyelesaian di bawah.
Mencari nilai x’:

Mencari nilai y’:

Subtitusi persamaan x’ = 2y”‒ x” dan y’ = 3y” ‒ x” yang diperoleh pada persamaan ‒x’ + 3y’ ‒ 11 = 0. Hasil substitusi tersebut adalah persamaan garis karena transformasi oleh matriks A.
‒x’ + 3y’ ‒ 11 = 0
‒(2y’’ ‒ x’’) + 3(3y’’ ‒ x’’) ‒ 11 = 0
‒2y’’ + x’’ + 9y’’ ‒ 3x’’ ‒ 11 = 0
‒2x’’ + 7y’’ ‒ 11 = 0
2x’’ ‒ 7y’’ + 11 = 0
Jadi, persamaan garis 3x ‒ y ‒ 11 = 0 karena refleksi terhadap garis y = x, dilanjutkan oleh transformasi yang bersesuaian dengan matriks A adalah 2x ‒ 7y + 11 = 0.