Bahsan operasi hitung matriks meliputi bagaimana cara melakukan operasi hitung penjumlahan, pengurangan, dan perkalian pada matriks. Operasi hitung penjumlahan dan pengurangan pada dua buah matrik dapat dilakukan jika dua buah matriks tersebut memiliki ukuran yang sama. Ukuran matriks yang sama ditunjukkan dengan baris dan kolom pada matriks tersebut sama. Sedangkan pada perkalian matriks, operasi hitung dapat dilakukan jika matriks pertama memiliki jumlah kolom yang sama banyaknya dengan jumlah baris pada matriks ke dua.
Cara melakukan operasi hitung matriks pada penjumlahan dan pengurangan sangat sederhana yaitu dengan melakukan operasi hitung antar elemen dalam matriks. Jika sobat idschool sudah mengerti bagaimana cara menjumlahkan atau mengurangkan suatu bilangan, sobat idschool tidak akan kesulitan dalam menjumlahkan atau mengurangkan antar elemen matriks.
Untuk operasi hitung perkalian matriks memang sedikit lebih rumit, terlebih untuk matriks dengan ukuran matriks yang besar. Cara melakukan operasi hitung perkalian matriks perlu mengalikan setiap elemen baris matriks pertama dengan setiap elemen kolom matriks ke dua. Memang terlihat sedikit rumit, namun jangan khawatir, operasi hitungnya mudah dan sobat idschool hanya perlu lebih teliti dalam mengerjakannya.
Selanjutnya, mari kita simak pembahasan operasi hitung matriks dan sifat-sifatnya pada pembahasan di bawah.
Table of Contents
Baca Juga: Pengertian dan Jenis-jenis Matriks
1) Operasi Hitung Penjumlahan Matriks
Operasi hitung matriks pada penjumlahan memiliki syarat yang harus dipenuhi agar dua buah matriks dapay dijumlahkan. Syarat dari dua buah matriks atau lebih dapat dijumlahkan jika memiliki nilai ordo yang sama. Artinya, semua matriks yang dijumlahkan harus memiliki jumlah baris dan kolom yang sama.
Matriks dengan jumlah baris 3 dan kolom 4 hanya bisa dijumlahkan dengan matriks dengan jumlah baris 3 dan kolom 4. Matriks dengan jumlah baris 3 dan kolom 4 tidak bisa dijumlahkan dengan matriks dengan jumlah baris 4 dan kolom 3. Kesimpulannya, jumlah baris dan kolom antar dua matriks yang akan dijumlahkan harus sama.
Operasi hitung matriks untuk penjumlahan matriks memenuhi sifat komutatif, asosiatif, memiliki matriks identitas matriks nol, dan memiliki lawan matriks. Lawan matriks A adalah matriks ‒A, di mana elemen-elemen matriks ‒A merupakan lawan dari elemen-elemen matriks A.
Secara ringkas, sifat operasi penjumlahan matriks dapat dilihat pada gambar di bawah.

Selanjutnya, kita akan mempelajari cara melakukan operasi hitung penjumlahan dua buah matriks. Penjelasan akan diberikan dalam bentuk contoh soal secara umum seperti bentuk di bawah.
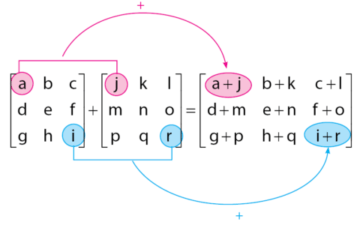
Baca Juga: Penggunaan Matriks untuk Menyelesaikan Sistem Persamaan Linear (SPL)
2) Operasi Hitung Matriks – Pengurangan
Seperti halnya operasi hitung penjumlahan matriks, syarat agar dapat mengurangkan elemen-elemen antar matriks adalah matriks harus memiliki nilai ordo yang sama. Cara melakukan operasi pengurangan pada matriks dapat dilihat seperti cara di bawah.
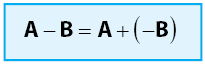
Cara melakukan operasi pengurangan dua matriks tidak jauh berbeda dengan penjumlahan matriks. Untuk lebih jelasnya, perhatikan contoh soal pengurangan matriks secara umum yang akan diberikan di bawah.
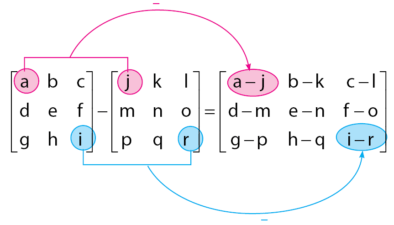
Baca Juga: Cara Menentukan Nilai x dan y (Variabel) pada Suatu Persamaan Matriks
3) Perkalian Matriks
Pembahasan operasi hitung matriks selanjutnya yang akan dibahas adalah perkalian matriks. Perkalian matriks yang akan dibahas di bawah adalah perkalian matriks dengan skalar dan perkalian matriks dengan matriks. Selengkapnya simak operasi hitung perkalian matriks di bawah.
Perkalian Matriks dengan Skalar
Cara melakukan operasi hitung matriks untuk perkalian matriks dengan skalar dilakukan dengan mengalikan semua elemen-elemen matriks dengan skalarnya. Jika k adalah suatu konstanta dan A adalah matriks, maka cara melakukan operasi perkalian skalar dapat dilihat melalui cara di bawah.
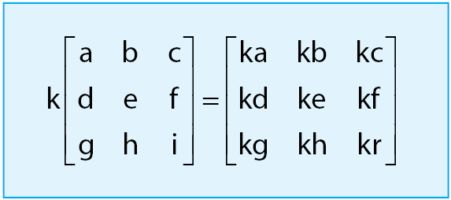
Cara melakukan perkalian matriks dengan skalar cukup mudah dilakukan. Contoh soal cara melakukan perkalian matriks yang akan diberikan di bawah akan menambah pemahaman sobat idschool.
Contoh cara melakukan operasi perkalian skalar pada matriks A dengan konstanta k = 2:

Operasi Perkalian Dua Matriks
Seperti yang telah disinggung sebelumnya, syarat dua buah matriks dapat dikalikan jika memiliki jumlah kolom matriks pertama yang sama dengan jumlah baris matriks ke dua. Ordo matriks hasil perkalian dua matriks adalah jumlah baris pertama dikali jumlah kolom ke dua.
Matriks A memiliki jumlah kolom sebanyak m dan jumlah baris r, matriks B memiliki jumlah kolom sebanyak r dan jumlah baris m, hasil perkalian matriks A dan B adalah matriks C dengan jumlah kolom m dan jumlah baris n.
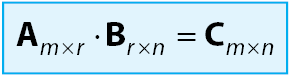
Sebelum mengulas cara melakukan operasi perkalian dua buah matriks, sebaiknya kita perlajari dahulu sidat-sifat operasi perkalian dua matriks. Sifat-sifat operasi perkalian matriks meliputi sifat asosiatif, distributif, dan memiliki matriks identitas I. Sifat-sifat operasi perkalian matriks dapat dilihat pada gambar di bawah.

Sifat-sifat matriks di atas dapat digunakan untuk memudahkan perhitungan dalam melakukan operasi hitung matriks.
Sekarang, pembahasan kita masuk pada perkalian dua matriks. Untuk pembahasan pertama kita akan mempelajari cara melakukan perkalian matriks dengan ukuran 2 × 2 dan matriks dengan ukuran 2 × 1. Proses cara melakukan operasi perkalian matriksdengan ukuran 2 × 2 dan matriks dengan ukuran 2 × 1 dapat disimak pada pembahasan di bawah.
Diketahui matriks A memiliki ukuran 2 × 2 dan matriks B memiliki ukuran 2 × 1. Perkalian antara matriks A dan matriks B dapat dilakukan seperti cara di bawah.
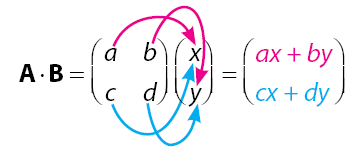
Selanjutnya adalah perkalian dua matriks. Kedua matriks yang akan dioperasikan sama-sama berukuran 2 × 2. Diketahui matriks P memiliki ukuran 2 × 2 dan matriks Q memiliki ukuran 2 × 2. Perkalian dua matriks P × Q dapat diperoleh dengan cara di bawah.
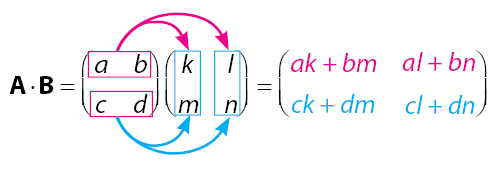
Untuk lebih jelasnya akan ditunjukkan dari contoh soal operasi perkalian dua matriks seperti yang ditunjukkan di bawah.
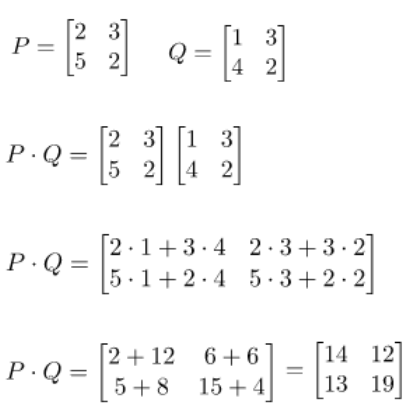
Sekian pembahasan mengenai operasi hitung matriks yang meliputi penjumlahan, pengurangan, dan perkalian matriks. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Menyelesaikan Sistem Persamaan Linear SPL dengan Matriks

Kalo operasi matriks a+b-c , mana dulu yang di selesaikan?
Halo Joni, penjumlahan dan pengurangan memiliki bobot yang seimbang yaa, sehingga pengerjaan bisa diselesaikan urut dari kiri.
kak, kalo matriks beda ordo bisa nggak ya di jumlahkan? kalao bisa gimana caranya?
Ga bisa, syarat penjumlahan matriks harus mempunyai ordo yang sama.