Perhatikan gambar di bawah!
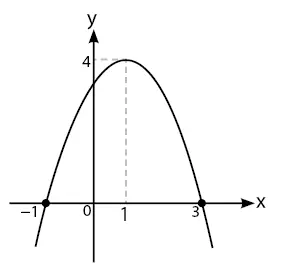
Persamaan yang sesuai dengan grafik fungsi kuadrat di atas adalah ….
A. y = x2 + 2x + 3
B. y = x2 ‒ 2x ‒ 3
C. y = ‒x2 + 2x ‒ 3
D. y = ‒x2 ‒ 2x + 3
E. y = ‒x2 + 2x + 3
Jawab: E
Dari gambar yang diberikan pada soal dapat diketahui bahwa kurva memotong sumbu x pada dua titik yaitu peroleh informasi x1 = ‒1 dan x2 = 3. Selain itu, dari gambar juga dapat diketahui titik puncak atau titik balik kurva yaitu (xp = 1, yp = 4).
Bentuk umum fungsi kurva parabola: y = a(x ‒ x1)(x ‒ x2)
Dari informasi yang diperoleh dapat dibentuk persamaan umum parabola yaitu y = a(x + 1)(x ‒ 3)
Substitusi nilai (xp = 1, yp = 4) ke persamaan untuk mendapatkan nilai a, seperti yang dilakukan pada cara berikut.
Menentukan nilai a:
yp = a(xp + 1)(xp ‒ 3)
4 = a(1 + 1)(1 ‒ 3)
4 = a·2·(‒2)
4 = ‒4a
a = 4/‒4 = ‒1
Cara menentukan persamaan kurva fungsi kuadrat:
y = a(x+1)(x‒3)
y = ‒1(x+1)(x‒3)
y = ‒1(x2‒3x+x‒3)
y = ‒1(x2‒2x‒ 3)
y = ‒x2 + 2x + 3
Jadi, persamaan yang sesuai dengan grafik fungsi kuadrat di atas adalah y = ‒x2 + 2x + 3.