Rini membeli 3 buku, 1 pensil, dan 2 penghapus seharga Rp39.000,00. Agus membeli 1 buku, 2 pensil, dan 3 penghapus seharga Rp26.000,00. Harga 1 buku 5000 lebih mahal daripada harga 1 pensil. Jika Dina membeli 2 buku, 4 pensil, dan 5 penghapus, maka dia harus membayar …  
(A)   Rp70.000,00
(B)   Rp65.000,00
(C)   Rp60.000,00
(D)   Rp55.000,00
(E)   Rp50.000,00

Jawab: (E)

Misalkan, harga buku = x; harga pensil = y; dan harga penghapus = z. Dari soal dapat dibentuk beberapa persamaan berikut.

• Persamaan (i)
  Rini membeli 3 buku, 1 pensil, dan 2 penghapus seharga Rp39.000,00 → 3x + y + 2z = 39.000

• Persamaan (ii)
  Agus membeli 1 buku, 2 pensil, dan 3 penghapus seharga Rp26.000,00 → x + 2y + 3z = 26.000

• Persamaan (iii)
  Harga 1 buku 5000 lebih mahal daripada harga 1 pensil → x = y + 5000

Diperoleh tiga pesamaan linear yaitu (i) 3x + y + 2z = 39.000; (ii) x + 2y + 3z = 26.000; dan (iii) x = y + 5.000. Harga buku (x), pensil (y), dan penghapus (z) dapat dicari tahu dengan menyelesaikan sistem persamaan linear tiga variabel (SPLTV) tersebut.

Pertama, eliminasi z dari persamaan (i) dan (ii):

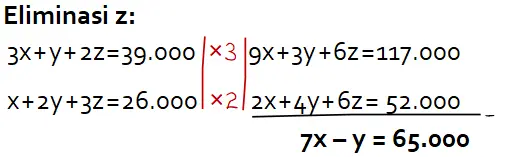
Diperoleh persamaan (iv) 7x – y = 65.000. Selanjutnya, substitusi persamaan (iii) x = y + 5.000 pada persamaan (iv) untuk mendapatkan nilai y (harga pensil) seperti yang dilakukan pada cara berikut.

Mneghitung nilai y:

7x – y = 65.000

7(y + 5.000) – y = 65.000

7y + 35.000 – y = 65.000

6y = 65.000 – 35.000 = 30.000

Menghitung nilai x:

x = y + 5.000

x = 5.000 + 5.000 = 10. 000

Menghitung nilai z:

x + 2y + 3z = 26.000

10.000 + 2(5.000) + 3z = 26.000

20.000 + 3z = 26.000

3z = 6.000

Dina membeli 2 buku, 4 pensil, dan 5 penghapus. Sehingga harga yang harus dibayar oleh Dina adalah 2x + 4y + 5z.

Harga yang harus dibayar oleh Dina:

= 2x + 4y + 5z

= 2(10.000) + 4(5.000) + 5(2.000)

= 20.000 + 20.000 + 10.000

= 50.000

Jadi, Dina harus membayar Rp50.000,00 (E).